연속 확률 변수Continuous random variable
연속 확률 변수Continuous random variable
📅
🚀
연속 확률 변수 (Continuous Random Variable) 🔗
무한한 범위의 값을 가질 수 있는 확률 변수
예시
- 버스가 도착하는 시간
- 주어진 시간 동안 파이프를 통해 흐르는 물의 양
- 무작위로 선택 된 사람의 키
성질
- 특정 값 에 대해 확률은 0이다.
🚀
확률 밀도 함수 (Probability Density Function, PDF) 🔗
연속 확률 변수의 경우 특정 값의 확률이 0이기 떄문에 확률 질량 함수를 사용할 수 없다. 따라서확률 밀도 함수(
: 연속적이고 비음수인 함수로서, 이 함수를 의
확률 밀도 함수
(PDF) 라고 한다.✅
예시 (확률 밀도 함수) 🔗
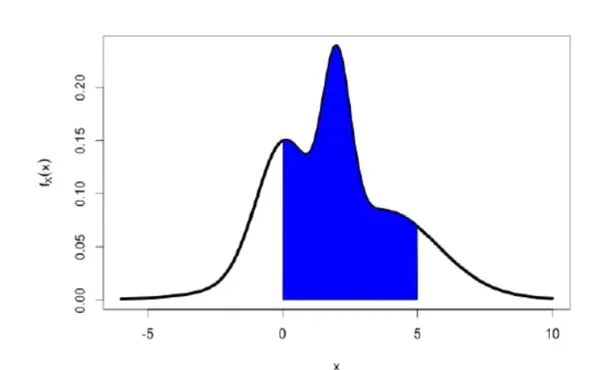
가 두 값 과 사이에 존재할 확률은 로 나타낼 수 있다.
더 일반적으로, 실선 상의 어떤 부분 집합 에 대하여
🚀
확률 법칙과 PDF (Probability Laws and PDF) 🔗
는 가 아님을 유의
특정 값 에 대해, 이다.
- 예를 들어, 를 의미
유효한 확률 법칙은 및 을 만족해야 한다. - 이는 PDF와 유사
- 정규화를 위해: 곡선 아래의 총 면적은 1이다
- 정규화를 위해: 는 비음수이므로, 모든 에 대하여 이다
확률 변수 길이가 인 작은 구간 에 대한 확률은 이다.
- 이는 가 에서의 밀도를 나타낸다.
🚀
PDF의 특성 (Properties of PDF) 🔗
를 PDF 를 가진 연속 확률 변수라고 하자.
- for all
- 가 매우 작으면,
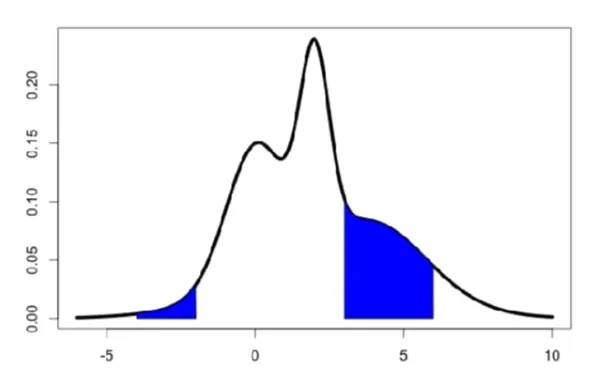
- 임의의 실수 부분집합 에 대하여,
✅
예시 🔗
🚀
연속 확률 변수의 기대값 (Expectation of Continuous Random Variable) 🔗
이산 확률 변수의 경우 우리는 다음과 같은 식을 사용했다.
가 연속 확률 변수이고 가 의 확률 밀도 함수라고 하자. 의 기대값은 다음과 같이 정의된다.
✅
예제 (연속 확률 변수의 기대값) 🔗
➡️
문제 🔗
가 구간에서의 균등 확률 변수라고 하자. 이때, 의 기댓값은 얼마인가?
➡️
해결 🔗
의 확률 밀도 함수는 다음과 같다.
의 기댓값은 다음과 같이 계산된다.
따라서, 의 기댓값은 이다.
🚀
연속 확률 변수의 분산 (Variance of Continuous Random Variable) 🔗
이산 확률 변수의 경우 우리는 다음과 같은 식을 사용했다.
가 연속 확률 변수이고 가 의 확률 밀도 함수라고 하자. 의 분산은 다음과 같이 정의된다.
✅
예제 (연속 확률 변수의 분산) 🔗
➡️
문제 🔗
가 구간에서의 균등 확률 변수라고 하자. 이때, 의 분산은 얼마인가?
➡️
해결 🔗
의 확률 밀도 함수는 다음과 같다.
의 분산은 다음과 같이 계산된다.
따라서, 의 분산은 이다.
🚀
지수 확률 변수 (Exponential Random Variable) 🔗
지수 확률 변수의 확률 밀도 함수는 다음과 같다.
가 특정 값을 초과할 확률은 지수적으로 감소한다는 점에 유의하라
✅
예시 (지수 확률 변수) 🔗
어떤 일이 일어날 때까지의 시간을 모델링하기 위해, 지수 확률 변수를 사용한다.
- 다음 이메일이 도착할 때까지의 시간
- 사고가 발생할 때까지의 시간
- 전구가 나갈 때까지의 시간
✅
예제 (지수 확률 변수) 🔗
➡️
문제 🔗
사하라 사막 어디든 작은 운석이 처음 떨어질 때까지의 시간은 평균 10일의 지수 확률 변수로 모델링된다.
현재 시간은 자정이다.
첫날 오전 6시에서 오후 6시 사이에 운석이 처음 떨어질 확률은 얼마인가?
➡️
해결 🔗
를 운석이 처음 떨어지는 시간이라고 하자.
는 평균 10일의 지수 확률 변수이므로, 이다.
첫날 오전 6시에서 오후 6시 사이에 운석이 처음 떨어질 확률은 다음과 같이 계산된다.
🚀
요약 (Summary) 🔗
연속 확률 변수
for all
가 매우 작을 때,
임의의 실수 부분집합 에 대하여, 기대값
분산
🚀
추가 문제 🔗
➡️
문제 🔗
연속 확률 변수 의 기댓값이 다음을 만족함을 보여라
➡️
해결 🔗
따라서,