일반적인 확률 변수

🚀

누적 분포 함수: CDF (Culmulative Distribution Function, CDF) 🔗

$P(X = x)$ 대신 $P(X \leq x)$ 가 필요할 때 사용

예시

버스가 1시 30분 전에 도착할 확률은 얼마인가?
무작위로 선택된 사람이 키가 5피트 7인치 이하일 확률은 얼마인가?
이번 달 강수량이 3인치 미만일 확률은 얼마인가?

확률 변수

X

의 CDF는

F_X

로 표기되며

P(X \leq x)

의 확률을 제공한다.

F_X(x) = P(X \leq x) = \begin{cases} \sum_{k \leq x} p_X(k) & X \text{가 이산형일 때} \\ \int_{-\infty}^{x} f_X(t) dt & X \text{가 연속형일 때}\\ \end{cases}

🚀

이산 확률 변수의 CDF (Discrete Random Variable: CDF) 🔗

$X$ 가 이산형일 때, $F_X(x)$ 는 $x$ 의 구간마다 일정한 값을 가지는 함수

F_X(x) = P(X \leq x) = \sum_{k \leq x} p_X(k)

🚀

연속 확률 변수의 CDF (Continuous Random Variable: CDF) 🔗

$X$ 가 연속형일 때, $F_X(x)$ 는 $x$ 의 연속 함수

F_X(x) = P(X \leq x) = \int_{-\infty}^{x} f_X(t) dt

CDF는 단조 증가(monotonically increasing)하다

$k \leq k' \Rightarrow F_X(k) \leq F_X(k')$

F_X(k)

는

k \to -\infty

일 때 0,

k \to \infty

일 때 1에 수렴한다.

✅

예제 (구간별 상수 확률 밀도 함수) 🔗

➡️

문제 🔗

알빈의 출근 시간은 15분에서 20분 사이일 확률이 2/3이고, 20분에서 25분 사이일 확률이 1/3이다. 각각의 시간은 동일한 확률로 발생한다. PDF를 작성할 수 있는가?

CDF는 어떻게 되는가?

➡️

해결 🔗

PDF

P(15 \leq X < 20) = 2/3 = 5p \Rightarrow p = 2/15

P(20 \leq X < 25) = 1/3 = 5p \Rightarrow p = 1/15

f_X(x) = \begin{cases} 2/15 & 15 \leq x < 20 \\ 1/15 & 20 \leq x < 25 \\ 0 & \text{otherwise} \end{cases}

CDF

- PDF를 적분하여 구할 수 있다.

F_X(x) = \int_{-\infty}^{x} f_X(t) dt = \begin{cases} 2/15(x-15) & 15 \leq x < 20 \\ 1/15(x-20) + 2/3 & 20 \leq x < 25 \\ 1 & x \geq 25 \end{cases}

🚀

정규 확률 변수 (Normal Random Variable) 🔗

연속 확률 변수 $X$ 가 다음 형태의 PDF를 가지면 정규 분포 또는 가우시안 분포를 따른다고 한다.
$f_X(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-(x-\mu)^2/2\sigma^2}$

평균: E[X] =

\mu

분산: var(X) =

\sigma^2

🚀

정규 확률 변수의 특징 1. 대칭성 (Symmetry of Normal Random Variable) 🔗

정규 확률 변수는 평균 $\mu$ 를 중심으로 대칭이다.

F_X(\mu + x) = 1 - F_X(\mu - x)

🚀

정규 확률 변수의 특징 2. 선형 변환 (Linear Transformation of Normal Random Variable) 🔗

$X$ 가 정규 분포를 따르면, $Y = aX + b$ 도 정규 분포를 따른다.

평균: E[Y] =

a\mu + b

분산: var(Y) =

a^2\sigma^2

🚀

정규 확률 변수의 특징 3. 표준 정규 확률 변수 (Standard Normal Random Variable) 🔗

평균이 0이고 분산이 1인 정규 확률 변수를 표준 정규 확률 변수라고 한다.

표준화

X

가 평균

\mu

와 분산

\sigma^2

를 가진 정규 확률 변수라고 하자. 우리는

X

를 다음과 같이 표준 정규 확률 변수

Y

로 표준화한다.

Y = \frac{X - \mu}{\sigma}

✅

증명 (표준 정규 확률 변수) 🔗

정규 확률 변수

X

가 주어졌을 때,

$E[X] = \mu, \quad \text{var}(X) = \sigma^2$

표준화를 통해,

$Y = \frac{X - \mu}{\sigma}$
$Y$ 는 평균 $\mu = 0$ 및 분산 $\sigma^2 = 1$ 을 가지는
표준 정규 확률 변수
가 된다.

증명:

Y

가

X

의 선형 변환이기 때문에,

Y

는 정규 분포를 따른다. 더불어,

$E[Y] = \frac{E[X] - \mu}{\sigma} = 0$
$\text{var}(Y) = \frac{\text{var}(X)}{\sigma^2} = 1$

따라서,

Y

는 표준 정규 확률 변수다.

🚀

표준 정규 확률 변수의 CDF (CDF of Standard Normal Random Variable) 🔗

표준 정규 확률 변수 $Y$ 의 CDF는 $\Phi(y)$ 로 표기한다.

Y

가 표준 정규 확률 변수일 때,

Y

의 CDF는 다음과 같다.

\Phi(y) = P(Y \leq y) = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{y} e^{-t^2/2} dt

이를 분석적으로 계산할 수 없다.
대신, 표준 정규 분포표를 사용하여 $y \geq 0$ 일 때 $\Phi(y)$ 값을 확인한다.

✅

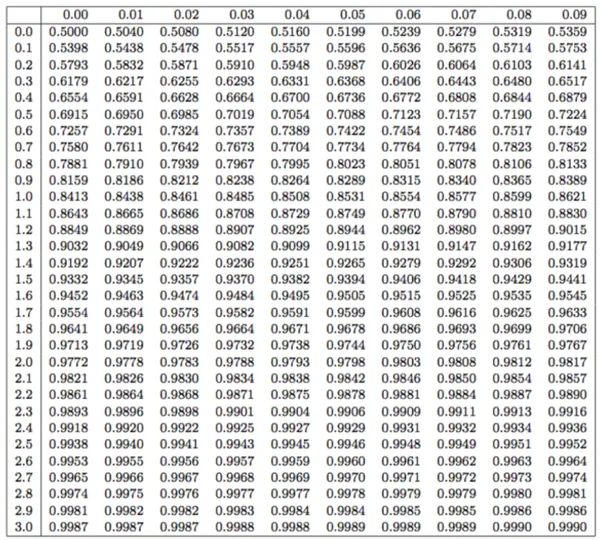
예시 (표준 정규 분포표) 🔗

	.00	.01	.02	.03	.04	...
0.0	0.5000	0.5040	0.5080	0.5120	0.5160	...
0.1	0.5398	0.5438	0.5478	0.5517	0.5557	...
0.2	0.5793	0.5832	0.5871	0.5910	0.5948	...
0.3	0.6179	0.6217	0.6255	0.6293	0.6331	...
...	...	...	...	...	...	...

$\Phi(0.21) = P(Y < 0.21) = 0.5832$
$\Phi(0.1) = P(Y < 0.1) = 0.5398$
$\Phi(-0.1) = P(Y < -0.1) = P(Y > 0.1) = 1 - P(Y < 0.1) = 1 - \Phi(0.1) = 1 - 0.5398 = 0.4602$

✅

예제 (표준 정규 확률 변수의 CDF) 🔗

➡️

문제 🔗

특정 지역의 연간 강설량은 평균

\mu = 60

인치, 표준 편차

\sigma = 20

인 정규 확률 변수로 모델링된다. 올해의 강설량이 최소 80인치일 확률은 얼마인가?

➡️

해결 🔗

$X$ 를 연간 강설량으로 정의한다.
$P(X \geq 80)$ 를 계산해야 한다. 이는 CDF다.
CDF는 표준 정규 분포표를 사용하여 효율적으로 계산할 수 있다.
주의: 표준 정규 분포표는 $X$ 가 표준 정규 확률 변수일 때만 사용할 수 있다.
$X$ 는 표준 정규 확률 변수가 아니므로 표준화가 필요하다.

표준화를 통해, 표준 정규 확률 변수

Y

를 구한다.

Y = \frac{X - \mu}{\sigma} = \frac{X - 60}{20}

그러면

P(X \geq 80) = P\left( \frac{X - 60}{20} \geq \frac{80 - 60}{20} \right) = P(Y \geq 1) = 1 - P(Y \leq 1) = 1 - \Phi(1)

1 - \Phi(1) = 1 - 0.8413 = 0.1587

🚀

요약 (Summary) 🔗

정규 확률 변수

(Normal Random Variable)

연속 확률 변수

X

가 다음 형태의 PDF를 가지면 정규 분포 또는 가우시안 분포를 따른다고 한다.

$f_X(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{-(x-\mu)^2 / 2\sigma^2}$

여기서

\mu

와

\sigma^2

는 각각 평균과 분산으로, PDF를 특징짓는다.

$E[X] = \mu$
$\text{var}(X) = \sigma^2$

표준화

(Standardization)

X

가 평균

\mu

와 분산

\sigma^2

를 가지는 정규 확률 변수라고 하자. 우리는

X

를 표준 정규 확률 변수

Y

로 표준화할 수 있다.

$Y = \frac{X - \mu}{\sigma}$

🚀

추가 문제 🔗

➡️

문제 🔗

X

가 평균이 0이고 표준 편차가

\sigma

인 정규 확률 변수라고 하자.

표준 정규 분포표를 사용하여 다음 사건의 확률을 계산하라:

\{ X \geq k\sigma \}

및

\{ |X| \leq k\sigma \}

for

k = 1, 2, 3

➡️

해결 🔗

Z

를 표준 정규 확률 변수로 정의하자.

$Z = \frac{X - \mu}{\sigma} = \frac{X - 0}{\sigma} = \frac{X}{\sigma} = \frac{X}{\sigma}$

P(X \geq k\sigma) = P\left( Z \geq k \right) = 1 - P(Z \leq k) = 1 - \Phi(k)

표에 의하면,

\Phi(1) = 0.8413, \quad \Phi(2) = 0.9772, \quad \Phi(3) = 0.9986

P(X \geq \sigma) = 1 - 0.8413 = 0.1587

P(X \geq 2\sigma) = 1 - 0.9772 = 0.0228

P(X \geq 3\sigma) = 1 - 0.9986 = 0.0014

P(|X| \leq k\sigma) = P(-k\sigma \leq X \leq k\sigma) = P\left( -k \leq \frac{X}{\sigma} \leq k \right) = P\left( -k \leq Z \leq k \right) = \Phi(k) - \Phi(-k) = \Phi(k) - (1 - \Phi(k)) = 2\Phi(k) - 1

P(|X| \leq \sigma) = 2\Phi(1) - 1 = 2(0.8413) - 1 = 0.6826

P(|X| \leq 2\sigma) = 2\Phi(2) - 1 = 2(0.9772) - 1 = 0.9544

P(|X| \leq 3\sigma) = 2\Phi(3) - 1 = 2(0.9986) - 1 = 0.9972

추천 포스트

일반적인 확률 변수Normal Random Variable

누적 분포 함수: CDF (Culmulative Distribution Function, CDF) 🔗

이산 확률 변수의 CDF (Discrete Random Variable: CDF) 🔗

연속 확률 변수의 CDF (Continuous Random Variable: CDF) 🔗

예제 (구간별 상수 확률 밀도 함수) 🔗

문제 🔗

해결 🔗

정규 확률 변수 (Normal Random Variable) 🔗

정규 확률 변수의 특징 1. 대칭성 (Symmetry of Normal Random Variable) 🔗

정규 확률 변수의 특징 2. 선형 변환 (Linear Transformation of Normal Random Variable) 🔗

정규 확률 변수의 특징 3. 표준 정규 확률 변수 (Standard Normal Random Variable) 🔗

증명 (표준 정규 확률 변수) 🔗

표준 정규 확률 변수의 CDF (CDF of Standard Normal Random Variable) 🔗

예시 (표준 정규 분포표) 🔗

예제 (표준 정규 확률 변수의 CDF) 🔗

문제 🔗

해결 🔗

요약 (Summary) 🔗

추가 문제 🔗

문제 🔗

해결 🔗

일반적인 확률 변수
Normal Random Variable