PromleeBlog
sitemap
aboutMe

posting thumbnail
컨볼루션
Convolutions

📅
🚀 컨볼루션 신경망
🚀 컨볼루션: 이산 경우
✅ 증명
✅ 예제
🚀 컨볼루션: 연속 경우
✅ 증명
✅ 예제
🚀 컨볼루션의 그래픽 계산
✅ 예제
🚀 요약
🚀 추가 문제
🚀

컨볼루션 신경망 (Convolutional Neural Network, CNN) 🔗

컨볼루션 신경망(CNN)은 이미지 인식 및 분류 작업에 주로 사용되는 심층 학습 모델이다.
CNN은 여러 개의 컨볼루션 계층과 풀링 계층으로 구성되어 있다.
각 계층은 입력 이미지에서 중요한 특징을 추출하고 이를 계층적으로 축적한다.
🚀

컨볼루션: 이산 경우 (Convolutions: Discrete Case) 🔗

W=X+YW = X + Y이며 XX와 YY는 확률 질량 함수(PMF) pX(x)p_X(x)와 pY(y)p_Y(y)를 가지는 독립적인 이산 확률 변수다.
그러면, 임의의 정수 ww에 대해,
pW(w)=P(X+Y=w)=∑xpX(x)pY(w−x)p_W(w) = P(X + Y = w) = \sum_x p_X(x) p_Y(w - x)
결과적으로 얻어지는 PMF pW(w)p_W(w)는 XX와 YY의 PMF의 컨볼루션이라 한다.
✅

증명 (컨볼루션: 이산 경우) 🔗

임의의 정수 ww에 대해,
pW(w)=P(W=w)=P(X+Y=w)=∑xP(X=x,Y=w−x)p_W(w) = P(W = w) = P(X + Y = w) = \sum_x P(X = x, Y = w - x)
=∑xpX(x)pY(w−x)= \sum_x p_X(x) p_Y(w - x)
✅

예제 (컨볼루션: 이산 경우) 🔗

➡️

문제 🔗

XX와 YY가 독립이고 각각 다음과 같은 PMF를 가질 때,
pX(x)={13if x=1,2,3,0otherwisep_X(x) = \begin{cases} \frac{1}{3} & \text{if } x = 1, 2, 3, \\ 0 & \text{otherwise} \end{cases}
pY(y)={12if y=0,13if y=1,16if y=2,0otherwisep_Y(y) = \begin{cases} \frac{1}{2} & \text{if } y = 0, \\ \frac{1}{3} & \text{if } y = 1, \\ \frac{1}{6} & \text{if } y = 2, \\ 0 & \text{otherwise} \end{cases}
컨볼루션을 통해 W=X+YW = X + Y의 PMF를 계산하라.
➡️

해결 🔗

pW(1)=∑pX(x)pY(1−x)=pX(1)⋅pY(0)=13⋅12=16p_W(1) = \sum p_X(x) p_Y(1 - x) = p_X(1) \cdot p_Y(0) = \frac{1}{3} \cdot \frac{1}{2} = \frac{1}{6}
pW(2)=pX(1)⋅pY(1)+pX(2)⋅pY(0)=13⋅13+13⋅12=19+16=518p_W(2) = p_X(1) \cdot p_Y(1) + p_X(2) \cdot p_Y(0) = \frac{1}{3} \cdot \frac{1}{3} + \frac{1}{3} \cdot \frac{1}{2} = \frac{1}{9} + \frac{1}{6} = \frac{5}{18}
pW(3)=pX(1)⋅pY(2)+pX(2)⋅pY(1)+pX(3)⋅pY(0)=13⋅16+13⋅13+13⋅12=118+19+16=13p_W(3) = p_X(1) \cdot p_Y(2) + p_X(2) \cdot p_Y(1) + p_X(3) \cdot p_Y(0) = \frac{1}{3} \cdot \frac{1}{6} + \frac{1}{3} \cdot \frac{1}{3} + \frac{1}{3} \cdot \frac{1}{2} = \frac{1}{18} + \frac{1}{9} + \frac{1}{6} = \frac{1}{3}
pW(4)=pX(2)⋅pY(2)+pX(3)⋅pY(1)=13⋅16+13⋅13=118+19=16p_W(4) = p_X(2) \cdot p_Y(2) + p_X(3) \cdot p_Y(1) = \frac{1}{3} \cdot \frac{1}{6} + \frac{1}{3} \cdot \frac{1}{3} = \frac{1}{18} + \frac{1}{9} = \frac{1}{6}
pW(5)=pX(3)⋅pY(2)=13⋅16=118p_W(5) = p_X(3) \cdot p_Y(2) = \frac{1}{3} \cdot \frac{1}{6} = \frac{1}{18}
🚀

컨볼루션: 연속 경우 (Convolutions: Continuous Case) 🔗

W=X+YW = X + Y이며 XX와 YY는 확률 밀도 함수(PDF) fX(x)f_X(x)와 fY(y)f_Y(y)를 가지는 독립적인 연속 확률 변수다.
그러면, 임의의 실수 ww에 대해,
fW(w)=∫−∞∞fX(x)fY(w−x) dx=∫−∞∞fX(w−y)fY(y) dyf_W(w) = \int_{-\infty}^{\infty} f_X(x) f_Y(w - x) \, dx = \int_{-\infty}^{\infty} f_X(w - y) f_Y(y) \, dy
결과적으로 얻어지는 PDF fW(w)f_W(w)는 XX와 YY의 PDF의 컨볼루션이라 한다.
✅

증명 (컨볼루션: 연속 경우) 🔗

임의의 실수 ww에 대해,
FW(w)=P(W≤w)=P(X+Y≤w)=∫x=−∞∞∫y=−∞w−xfX(x)fY(y) dy dx=∫x=−∞∞fX(x)[∫y=−∞w−xfY(y) dy] dx=∫x=−∞∞fX(x)FY(w−x) dxF_W(w) = P(W \leq w) = P(X + Y \leq w)\\ = \int_{x=-\infty}^{\infty} \int_{y=-\infty}^{w-x} f_X(x) f_Y(y) \, dy \, dx\\ = \int_{x=-\infty}^{\infty} f_X(x) \left[ \int_{y=-\infty}^{w-x} f_Y(y) \, dy \right] \, dx\\ = \int_{x=-\infty}^{\infty} f_X(x) F_Y(w - x) \, dx\\

fW(w)=dFWdw(w)=ddw[∫x=−∞∞fX(x)FY(w−x) dx]=∫x=−∞∞fX(x)ddwFY(w−x) dx=∫x=−∞∞fX(x)fY(w−x) dxf_W(w) = \frac{dF_W}{dw}(w) = \frac{d}{dw} \left[ \int_{x=-\infty}^{\infty} f_X(x) F_Y(w - x) \, dx \right]\\ = \int_{x=-\infty}^{\infty} f_X(x) \frac{d}{dw} F_Y(w - x) \, dx\\ = \int_{x=-\infty}^{\infty} f_X(x) f_Y(w - x) \, dx\\
✅

예제 (컨볼루션: 연속 경우) 🔗

➡️

문제 🔗

XX와 YY는 독립적인 확률 변수다.
XX는 구간 [−2,2][-2, 2]에서 균등 분포를 따르고, YY는 구간 [−1,5][-1, 5]에서 균등 분포를 따른다.
Z=X+YZ = X + Y일 때, fZ(3)=16f_Z(3) = \frac{1}{6}이다.
참/거짓을 판단하라.
➡️

해결 🔗

fZ(z)=∫−∞∞fX(x)fY(z−x) dx=∫−∞∞fX(z−x)fY(x) dxfZ(3)=∫−∞∞fX(3−x)fY(x) dx=∫15(14)(16) dx=16f_Z(z) = \int_{-\infty}^{\infty} f_X(x) f_Y(z - x) \, dx = \int_{-\infty}^{\infty} f_X(z - x) f_Y(x) \, dx\\ f_Z(3) = \int_{-\infty}^{\infty} f_X(3 - x) f_Y(x) \, dx = \int_1^5 \left( \frac{1}{4} \right) \left( \frac{1}{6} \right) \, dx = \frac{1}{6}
따라서, 참이다.
🚀

컨볼루션의 그래픽 계산 (Graphic Calculation of Convolutions) 🔗

그림을 사용하여 컨볼루션을 계산할 수 있다.
예를 들어, 다음과 같은 컨볼루션 fW(w)=∫−∞∞fX(t)fY(w−t) dtf_W(w) = \int_{-\infty}^{\infty} f_X(t) f_Y(w - t) \, dt를 계산하라.
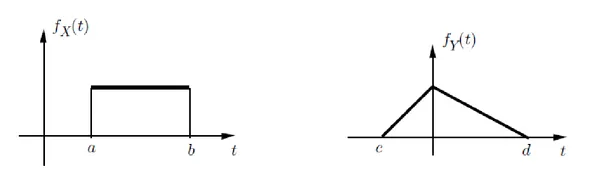
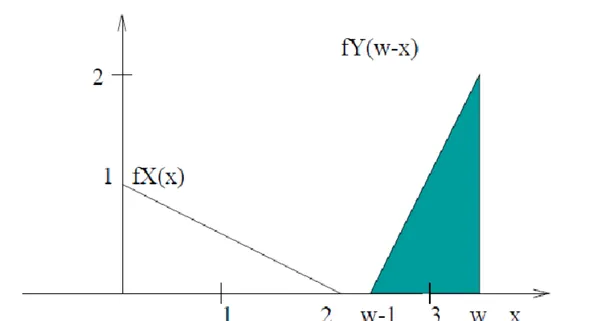
image
fY(w−t)f_Y(w - t): 이 그래프는 fY(t)f_Y(t)의 그래프와 같은 모양이지만 먼저 뒤집힌 다음 ww만큼 이동한 것이다.
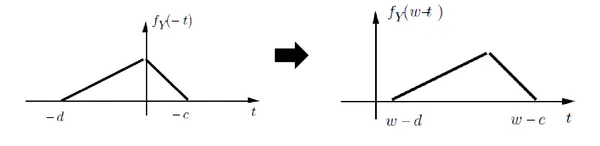
image
fX(t)fY(w−t)f_X(t) f_Y(w - t): 교차 구간을 찾아 두 그래프의 곱을 계산하라.
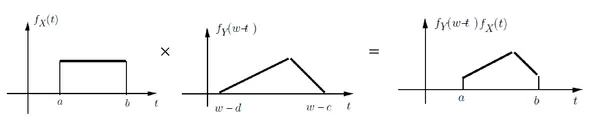
image
fW(w)=∫−∞∞fX(t)fY(w−t) dtf_W(w) = \int_{-\infty}^{\infty} f_X(t) f_Y(w - t) \, dt: fW(w)f_W(w)는 교차 구간의 곡선 아래의 전체 면적이다.
✅

예제 (컨볼루션의 그래픽 계산) 🔗

XX와 YY의 확률 밀도 함수는 다음과 같다. 컨볼루션을 계산하라.
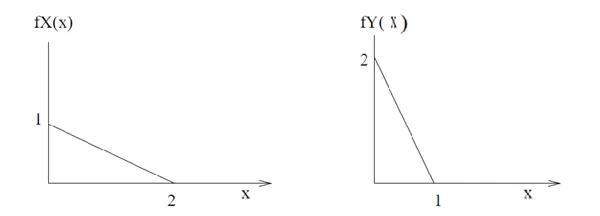
image
➡️

해결 🔗

w의 PDF: fW(w)=∫−∞∞fX(x)fY(w−x) dxf_W(w) = \int_{-\infty}^{\infty} f_X(x) f_Y(w - x) \, dx
  1. w≤0w \leq 0: fW(w)=0f_W(w) = 0
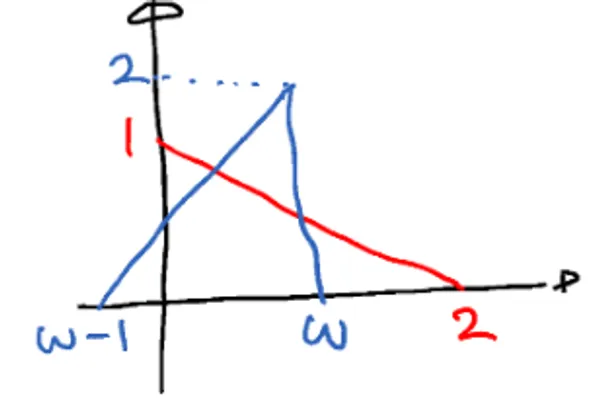
    image
  2. 0<w≤10 < w \leq 1: fW(w)=∫0wfX(x)fY(w−x) dx=2w−32w2+16w3f_W(w) = \int_{0}^{w} f_X(x) f_Y(w - x) \, dx = 2w - \frac{3}{2}w^2 + \frac{1}{6}w^3
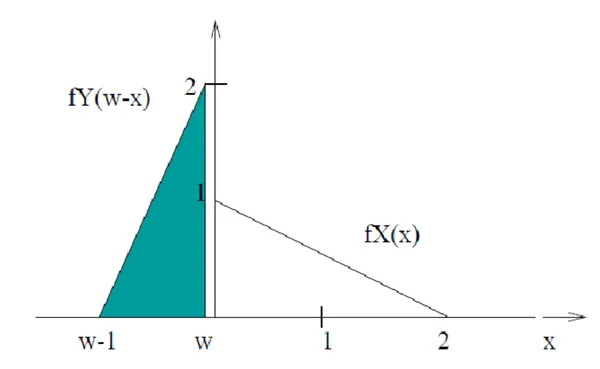
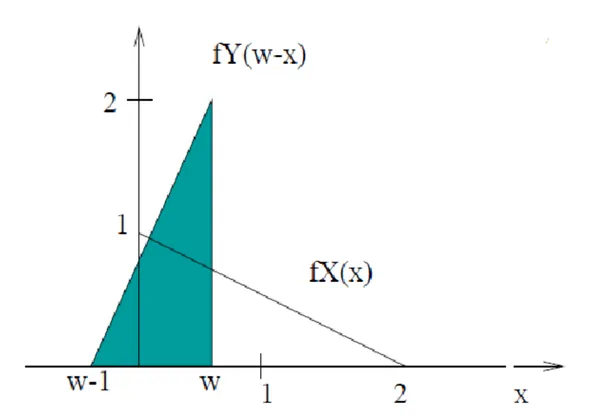
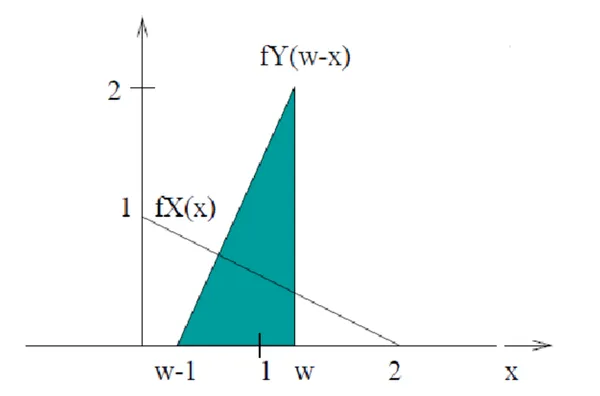
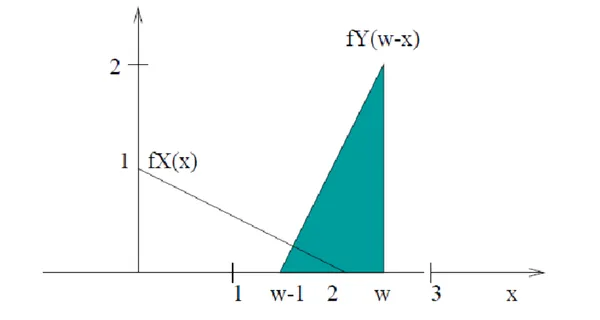
    image
  3. 1<w≤21 < w \leq 2: fW(w)=∫w−11fX(x)fY(w−x) dx=76−12wf_W(w) = \int_{w - 1}^{1} f_X(x) f_Y(w - x) \, dx = \frac{7}{6} - \frac{1}{2}w
    image
  4. 2<w≤32 < w \leq 3: fW(w)=∫w−12fX(x)fY(w−x) dx=92−92w+32w2−16w3f_W(w) = \int_{w - 1}^{2} f_X(x) f_Y(w - x) \, dx = \frac{9}{2} - \frac{9}{2} w + \frac{3}{2} w^2 - \frac{1}{6} w^3
    image
  5. w>3w > 3: fW(w)=0f_W(w) = 0
    image

2번 예시
image
fX(x)=−12x+1f_X(x) = -\frac{1}{2}x + 1
fY(w−x)=2x−2w+2f_Y(w-x) = 2x - 2w + 2
fW(w)=∫0w(−12x+1)(2x−2w+2) dx=2w−32w2+16w3f_W(w) = \int_{0}^{w} (-\frac{1}{2}x + 1)(2x - 2w + 2) \, dx = 2w - \frac{3}{2}w^2 + \frac{1}{6}w^3
🚀

요약 (Summary) 🔗

연속 확률 변수의 컨볼루션
(Convolution of Continuous Random Variables)
이산 확률 변수의 컨볼루션
(Convolution of Discrete Random Variables)
🚀

추가 문제 🔗

➡️

문제 🔗

임의 변수 XX, YY, ZZ는 독립적이며 0과 1 사이에서 균등 분포를 따른다.
W=X+Y+ZW = X + Y + Z의 확률 밀도 함수(PDF)를 구하라.
➡️

해결 🔗

V = X + Y 🔗
V=X+YV = X + Y의 확률 밀도 함수(PDF)는 다음과 같다.
fV(v)=∫−∞∞fX(x)fY(v−x) dxf_V(v) = \int_{-\infty}^{\infty} f_X(x) f_Y(v - x) \, dx
  1. v<0v < 0: fV(v)=0f_V(v) = 0
  2. 0≤v≤10 \leq v \leq 1: fV(v)=∫0v1 dx=vf_V(v) = \int_{0}^{v} 1 \, dx = v
  3. 1≤v≤21 \leq v \leq 2: fV(v)=∫v−111 dx=2−vf_V(v) = \int_{v - 1}^{1} 1 \, dx = 2 - v
  4. v>2v > 2: fV(v)=0f_V(v) = 0
fV(v)={vif 0≤v≤1,2−vif 1≤v≤2,0otherwisef_V(v) = \begin{cases} v & \text{if } 0 \leq v \leq 1, \\ 2 - v & \text{if } 1 \leq v \leq 2, \\ 0 & \text{otherwise} \end{cases}



W = V + Z 🔗
W=V+ZW = V + Z의 확률 밀도 함수(PDF)는 다음과 같다.
fW(w)=∫−∞∞fV(v)fZ(w−v) dvf_W(w) = \int_{-\infty}^{\infty} f_V(v) f_Z(w - v) \, dv
  1. w<0w < 0: fW(w)=0f_W(w) = 0
  2. 0≤w≤10 \leq w \leq 1: fW(w)=∫0wv dv=12w2f_W(w) = \int_{0}^{w} v \, dv = \frac{1}{2}w^2
  3. 1≤w≤21 \leq w \leq 2: fW(w)=∫w−11v dv+∫1w(2−v) dv=1−(w−1)22−(2−w)22f_W(w) = \int_{w - 1}^{1} v \, dv + \int_{1}^{w} (2 - v) \, dv = 1 - \frac{(w-1)^2}{2} - \frac{(2-w)^2}{2}
  4. 2≤w≤32 \leq w \leq 3: fW(w)=∫w−12(2−v) dv=(3−2)22f_W(w) = \int_{w - 1}^{2} (2 - v) \, dv = \frac{(3-2)^2}{2}
  5. w>3w > 3: fW(w)=0f_W(w) = 0
fW(w)={12w2if 0≤w≤1,1−(w−1)22−(2−w)22if 1≤w≤2,(3−w)22if 2≤w≤3,0otherwisef_W(w) = \begin{cases} \frac{1}{2}w^2 & \text{if } 0 \leq w \leq 1, \\ 1 - \frac{(w-1)^2}{2} - \frac{(2-w)^2}{2} & \text{if } 1 \leq w \leq 2, \\ \frac{(3-w)^2}{2} & \text{if } 2 \leq w \leq 3, \\ 0 & \text{otherwise} \end{cases}