PromleeBlog
sitemap
aboutMe

posting thumbnail
공분산과 상관관계
Covariance and Correlation

📅
🚀 공분산
✅ 예시 1
✅ 예시 2
✅ 예제 1
🚀 공분산과 독립성
✅ 증명
🚀 공분산의 성질
🚀 공분산의 상관관계
✅ 예제
🚀 요약
🚀 추가 문제
🚀

공분산 (Covariance) 🔗

두 확률 변수 XX와 YY의 공분산은 다음과 같이 정의된다.
cov(X,Y)=E[(X−E[X])(Y−E[Y])]\text{cov}(X, Y) = E[(X - E[X])(Y - E[Y])]
같은 정의
Cov(X,Y)=E[(X−E[X])(Y−E[Y])]\text{Cov}(X, Y) = E[(X - E[X])(Y - E[Y])]
=E[XY−XE[Y]−YE[X]+E[X]E[Y]]= E[XY - XE[Y] - YE[X] + E[X]E[Y]]
=E[XY]−E[X]E[Y]= E[XY] - E[X]E[Y]
✅

예시 1 (공분산) 🔗

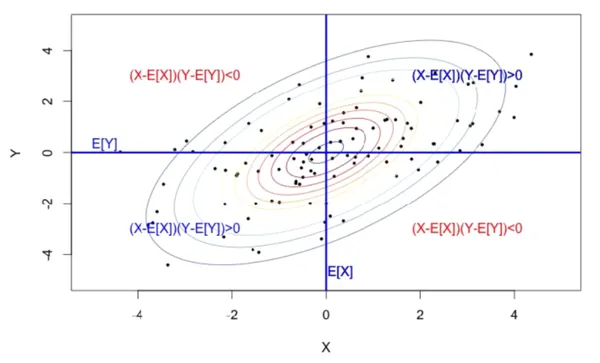
image
공분산이 양수이면, 대부분의 값이 오른쪽 상단과 왼쪽 하단 사분면에 위치한다.
공분산이 음수이면, 대부분의 값이 왼쪽 상단과 오른쪽 하단 사분면에 위치한다.
공분산이 0이면, 왼쪽 상단과 오른쪽 상단 사분면에 값이 거의 동일하게 분포한다.
✅

예시 2 (공분산) 🔗

아래에 두 개의 확률 변수 XX와 YY를 나타낸다.
어떤 그래프가 양의 공분산, 음의 공분산, 또는 0의 공분산에 해당하는지 확인하시오.
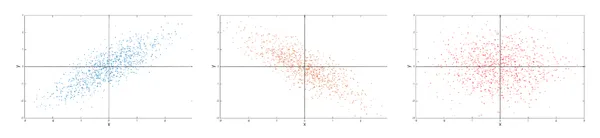
image
  1. 양의 공분산: 1번 그래프
  2. 음의 공분산: 2번 그래프
  3. 0의 공분산: 3번 그래프
✅

예제 1 (공분산) 🔗

➡️

문제 🔗

공평한 동전을 5번 던진다.
첫 번째 동전 던지기가 앞면이면 X=1X = 1, 그렇지 않으면 X=0X = 0이다.
YY를 앞면의 총 개수라고 하자.
XX와 YY 사이의 공분산은 무엇인가?
➡️

해결 🔗

E[X]=0.5E[X] = 0.5, E[Y]=5×0.5=2.5E[Y] = 5 \times 0.5 = 2.5이다.
E[XY]=∑x=01∑y=05xyPX,Y(x,y)=∑x=01∑y=05xyPX(x)PY∣X(y∣x)=12∑y=05yP(Y=y∣X=1)→E[XY] = \sum_{x=0}^{1} \sum_{y=0}^{5} xyP_{X,Y}(x,y) = \sum_{x=0}^{1} \sum_{y=0}^{5} xyP_X(x)P_{Y|X}(y|x)\\ = \frac{1}{2} \sum_{y=0}^{5} yP(Y = y | X = 1) \rightarrow 조건부 기댓값 E[Y∣X=1]E[Y | X = 1]로 표현된다.
만약 X=1X = 1이면, Y′Y'는 n=4n = 4와 p=12p = \frac{1}{2}인 이항 확률 변수이다.
따라서, E[Y∣X=1]=1+E[Y′]=1+42=3E[Y | X = 1] = 1 + E[Y'] = 1 + \frac{4}{2} = 3
그래서, E[XY]=32E[XY] = \frac{3}{2}
Cov(X,Y)=E[XY]−E[X]E[Y]=32−0.5×2.5=0.25\text{Cov}(X, Y) = E[XY] - E[X]E[Y] = \frac{3}{2} - 0.5 \times 2.5 = 0.25
따라서, XX와 YY 사이의 공분산은 0.25이다.
🚀

공분산과 독립성 (Covariance and Independence) 🔗

두 확률 변수 XX와 YY가 독립이면, Cov(X,Y)=0\text{Cov}(X, Y) = 0이다.
그러나, Cov(X,Y)=0\text{Cov}(X, Y) = 0이라고 해서 XX와 YY가 독립이라는 보장은 없다.
✅

증명 🔗

두 확률 변수 XX와 YY가 독립이면, E[XY]=E[X]E[Y]E[XY] = E[X]E[Y]이다.
따라서, Cov(X,Y)=E[XY]−E[X]E[Y]=E[X]E[Y]−E[X]E[Y]=0\text{Cov}(X, Y) = E[XY] - E[X]E[Y] = E[X]E[Y] - E[X]E[Y] = 0이다.
🚀

공분산의 성질 (Properties of Covariance) 🔗

XX와 XX의 공분산은 무엇인가?
XX와 aYaY의 공분산은 무엇인가?
XX와 Y+bY + b의 공분산은 무엇인가?
🚀

공분산의 상관관계 (Correlation of Covariance) 🔗

상관계수 ρX,Y\rho_{X,Y}는 공분산을 표준화한 값이다.
ρX,Y=Cov(X,Y)Var(X)Var(Y)\rho_{X,Y} = \frac{\text{Cov}(X, Y)}{\sqrt{\text{Var}(X)\text{Var}(Y)}}
상관계수는 항상 −1≤ρX,Y≤1-1 \leq \rho_{X,Y} \leq 1 범위 내에 있다.
  1. ρX,Y=1\rho_{X,Y} = 1: 완전한 양의 선형 관계를 나타낸다.
  2. ρX,Y>0\rho_{X,Y} > 0: 양의 공분산을 나타낸다.
  3. ρX,Y<0\rho_{X,Y} < 0: 음의 공분산을 나타낸다.
  4. ρX,Y=0\rho_{X,Y} = 0: 두 변수가 독립이다.
상관계수의 크기는 두 변수 간의 관계의 강도를 나타낸다.
✅

예제 (공분산의 상관관계) 🔗

➡️

문제 🔗

∣ρ∣=1|\rho| = 1인 경우는 XX와 YY 사이에 선형 관계가 있을 때에 한한다.
동전이 앞면이 나올 확률이 pp인 편향된 동전을 nn번 던진다.
XX를 앞면의 개수로, YY를 뒷면의 개수로 하자.
그러면 XX와 YY는 X=n−YX = n - Y와 같은 선형 관계를 가진다.
ρX,Y\rho_{X,Y}를 계산하시오.
➡️

해결 🔗

E[X]=npE[X] = np, E[Y]=n(1−p)=n−E[X]E[Y] = n(1 - p) = n - E[X]이다.
var(X)=np(1−p)=var(Y)\text{var}(X) = np(1 - p) = \text{var}(Y)이다.
모든 가능한 쌍 (x,y)(x, y)는 x+y=n=E[X]+E[Y]x + y = n = E[X] + E[Y]를 만족해야 한다.
따라서 x−E[X]=−(y−E[Y])x - E[X] = -(y - E[Y])이다.
따라서 (x−E[X])(y−E[Y])=−(x−E[X])2(x - E[X])(y - E[Y]) = -(x - E[X])^2이다.

다음을 알고 있다:
cov(X,Y)=E[(X−E[X])(Y−E[Y])]=−E[(X−E[X])2]=−var(X)\text{cov}(X, Y) = E[(X - E[X])(Y - E[Y])] = -E[(X - E[X])^2] = -\text{var}(X)
따라서 상관계수는 다음과 같다:
ρX,Y=cov(X,Y)var(X)var(Y)=−var(X)var(X)var(X)=−1\rho_{X,Y} = \frac{\text{cov}(X, Y)}{\sqrt{\text{var}(X) \text{var}(Y)}} = \frac{-\text{var}(X)}{\sqrt{\text{var}(X) \text{var}(X)}} = -1
🚀

요약 (Summary) 🔗

기댓값은 평균적으로 확률 변수가 어느 위치에 있을지 예측하는 값이다.
분산은 확률 변수가 기댓값으로부터 얼마나 떨어져 있을지를 측정하는 값이다.
두 확률 변수가 있을 때, 공분산은 두 변수 간 관계의 강도와 방향을 측정하는 값이다.
상관계수는 공분산의 표준화된 형태로, -1에서 1 사이의 값을 가지며 해석하기 쉽다.
XX와 YY가 독립이면, 공분산은 0이다. 그러나, 공분산이 0이라고 해서 항상 두 변수가 독립인 것은 아니다.
🚀

추가 문제 🔗

➡️

문제 🔗

슈바르츠 부등식. XX와 YY가 확률 변수일 때,
(E[XY])2≤E[X2]E[Y2](E[XY])^2 \leq E[X^2]E[Y^2]
➡️

해결 🔗

우리는 다음을 갖는다:
0≤E[(X−E[XY]E[Y2]Y)2]0 \leq E \left[ \left( X - \frac{E[XY]}{E[Y^2]} Y \right)^2 \right]
이를 전개하면 다음과 같다:
E[X2−2E[XY]E[Y2]XY+(E[XY]E[Y2]Y)2Y2]E \left[ X^2 - 2 \frac{E[XY]}{E[Y^2]} XY + \left( \frac{E[XY]}{E[Y^2]} Y \right)^2 Y^2 \right]
이를 각 항에 대해 적분하면:
E[X2]−2E[XY]E[Y2]E[XY]+E[XY]2E[Y2]2E[Y2]E[X^2] - 2 \frac{E[XY]}{E[Y^2]} E[XY] + \frac{E[XY]^2}{E[Y^2]^2} E[Y^2]
각 항을 단순화하면:E[X2]−2E[XY]2E[Y2]+E[XY]2E[Y2]E[X^2] - 2 \frac{E[XY]^2}{E[Y^2]} + \frac{E[XY]^2}{E[Y^2]}
따라서 다음을 얻는다:E[X2]−E[XY]2E[Y2]E[X^2] - \frac{E[XY]^2}{E[Y^2]}
이로부터,0≤E[X2]−E[XY]2E[Y2]0 \leq E[X^2] - \frac{E[XY]^2}{E[Y^2]}
따라서,E[XY]2E[Y2]≤E[X2]\frac{E[XY]^2}{E[Y^2]} \leq E[X^2]
양변에 E[Y2]E[Y^2]를 곱하면,(E[XY])2≤E[X2]E[Y2](E[XY])^2 \leq E[X^2]E[Y^2]
이로써 Schwartz 부등식을 증명하였다.