RSA 암호화

RSA Encryption

• 1978년에 Rivest, Shamir, Adleman에 의해 설계되었다.
• 가장 인기 있고 널리 사용되는 공개 키 암호화 체계다.
• 인수 분해의 어려움에 기반하고 있다.
• 암호화 및 복호화 알고리즘은 모듈러 지수화로 이루어져 있다.
• 결정론적 암호화는 IND-XXX 보안을 달성할 수 없다.
• 실제로는 RSA 암호화의 변형(예: RSA-OAEP)을 사용한다.
• 양자 공격에 대해서는 안전하지 않다.

1. 두 개의 소수를 선택합니다. 이 두 소수를 p와 q라고 한다.
2. $N = p * q$를 계산합니다.
3. $\phi(N) = (p-1) * (q-1)$를 계산합니다. $\phi(N)$은 N과 서로소인 수의 개수를 의미함
   오일러 파이 함수
4. $e$를 선택합니다. $1 < e < \phi(N)$이며, $e$와 $\phi(N)$은 서로소여야 함.
5. $d$를 계산합니다. $d$는 $d * e \equiv 1 \pmod{\phi(N)}$을 만족하는 수이다.
   확장된 유클리드 알고리즘을 사용하여 계산
6. 공개키 $pk=(N, e)$이며, 개인키 $sk=d$이다.

• RSA 키 생성은 두 소수 $p$와 $q$를 선택하고, 이를 이용하여 공개 키 $(N, e)$와 개인 키 $d$를 생성하는 과정이다.
• $N$은 두 소수의 곱으로, RSA 암호화에서 중요한 모듈로 사용된다.
• $\phi(N)$은 오일러의 피 함수로, $N$과 서로소인 정수의 개수를 나타낸다.
• 공개 지수 $e$는 암호화에 사용되며, 개인 키 $d$와 함께 중요한 역할을 한다.
• $d \cdot e \equiv 1 \ (\text{mod} \ \phi(N))$는 개인 키와 공개 지수가 서로
  역원 관계
  임을 보장하는 식이다.
  • 이 식은 확장된 유클리드 알고리즘을 사용하여 계산된다.

• RSA 암호화는 공개 키 $e$와 모듈로 $N$을 사용하여 평문 $M$을 암호문 $C$로 변환하는 과정이다.
• RSA 복호화는 개인 키 $d$를 사용하여 암호문 $C$를 다시 평문 $M'$로 변환하는 과정이다.
• 암호화와 복호화 모두 모듈로 $N$을 기반으로 한 거듭제곱 연산을 필요로 하며, 이는 컴퓨터가 큰 수의 연산을 효율적으로 수행할 수 있게 해주는 중요한 알고리즘에 기초한다.

1. $p = 13, q = 17$
2. $N = 13 \times 17 = 221$
3. $\phi(N) = (13 - 1)(17 - 1) = 12 \times 16 = 192$
4. $e = 5$
5. $d = 77$ (즉, $5 \times 77 = 385 = 1 \mod 192$)

• $M = 3$
• $C = M^e = 3^5 = 243 = 22 \mod 221$

• $C = 22$
• $M' = C^d = 22^{77} = (22^7)^{11} = 61^{11} = 3 \mod 221$

• 공개 키 암호화 체계는 암호화와 복호화 과정을 거친 후 원래의 메시지를 정확히 복원할 수 있어야 한다.
• RSA 알고리즘은 이러한 정확성을 보장하기 위해 오일러의 정리와 같은 수학적 원리를 사용한다.
• RSA의 정확성은 암호화와 복호화 과정에서 발생하는 지수 연산을 정확하게 수행함으로써 보장된다.

• 일반적으로 공개 키 지수 $e$는 대략 $\log_2 N$-비트이다. 따라서 평균적으로 $1.5(\log_2 N)$번의 곱셈이 필요하다.
• 매우 작고 햄밍 가중치가 낮은 $e$를 선택한다. 예를 들어, $e = 3, 17, 2^{16} + 1$

• 개인 키 $d$는 거의 전체 비트 길이를 가지지만 $e$는 매우 작다.

• 개인 키 지수 $d$는 Coppersmith 공격에 의해 $N^{0.292}$보다 커야 한다. 따라서 매우 작은 $d$를 사용할 수 없다.
• 중국인의 나머지 정리(Chinese Remainder Theorem, CRT) 사용:
  1. 계산:
     • $d_p = d \mod (p - 1)$
     • $d_q = d \mod (q - 1)$
  2. 계산:
     • $C_{dp} = C^{d_p} \mod p$
     • $C_{dq} = C^{d_q} \mod q$
  3. 계산:
     • $M = C_{dp} \cdot q \cdot M_q + C_{dq} \cdot p \cdot M_p$
       이 과정은 중국인의 나머지 정리를 사용하여 최종 메시지 $M$을 계산한다.

• RSA 암호화의 속도를 높이기 위해서는 공개 키 지수 $e$를 가능한 작게 선택하는 것이 좋다.
• 햄밍 가중치가 낮은 $e$는 해당 이진수에서 1의 개수가 적은 것을 의미하며, 곱셈 연산의 횟수를 줄일 수 있다.
• 복호화의 빠른 속도를 위해서는 중국인의 나머지 정리를 사용하여 복호화 과정을 최적화하는 것이 중요하다.

• $M = C_{d_p} \cdot q \cdot M_q + C_{d_q} \cdot p \cdot M_p$
• $M = 3 \cdot 13 \cdot 4 + 3 \cdot 17 \cdot 10 = 666$
• $M = 666 \mod 221 = 3$

• RSA 알고리즘의 복호화 과정을 중국인의 나머지 정리(CRT)를 사용하여 효율적으로 계산할 수 있다.
• CRT를 사용하면 $p$와 $q$에서 각각 계산한 결과를 합쳐 최종 결과를 얻을 수 있다.

• RSA의 안정성은 두 소수 $p$와 $q$를 곱한 $N$을 인수분해하는 것이 어렵다는 것에 기반한다.

• 교과서적 RSA는 결정론적 암호화이다. $\rightarrow$ IND-CPA 보안을 달성할 수 없다.
• 교과서적 RSA는 동형성을 가지고 있다. $\rightarrow$ IND-CCA2 보안을 달성할 수 없다.
  • $C_1 = M_1^e \mod N$, $C_2 = M_2^e \mod N$이 주어졌을 때, $C_1 \cdot C_2 = (M_1 \cdot M_2)^e \mod N$이다.

RSA-OAEP는 RSA 암호화에 사용되는 패딩 방법 중 하나이다.

RSA-OAEP는 RSA 암호화의 보안성을 높이기 위해 개발된 방법으로, 무작위성과 해시 함수를 사용하여 패딩을 적용한다.

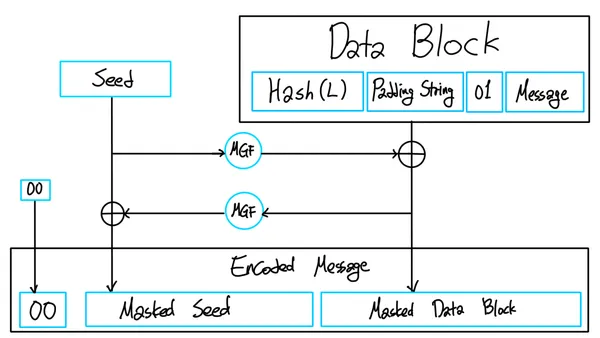
ss

1. $k - |M| -2|H| - 2$의 길이를 가진 문자열 PS(Padding String) 생성
2. 연결 - DB(Data Block) = $\text{Hash}(L)\; ||\; PS\; ||\; 0x01\; ||\; M$
3. $|H|$의 길이를 가진 무작위 바이트 문자열 Seed 생성
4. dbMask = $\text{MGF}(Seed, k - |H| - 1)$
5. MaskedDB = DB $\oplus$ dbMask
6. SeedMask = $\text{MGF}(dbMask, |H|)$
7. MaskedSeed = Seed $\oplus$ SeedMask
8. EM(Encoded Message) = $0x00 \;||\; MaskedSeed\; ||\; MaskedDB$