 서명 스키마Signature Schemes
서명 스키마Signature Schemes
📅
RSA 서명 (RSA Signature) 🔗
키 생성 (RSA) 🔗
- 두 소수 를 무작위로 선택, 로 설정
- 무작위 공개 지수 를 선택
- 를 만족하는 를 계산
- 공개 키 , 개인 키 를 반환
서명 (RSA) 🔗
메시지 에 대해 을 계산하여 서명 를 생성
검증 (RSA) 🔗
가 주어졌을 때, 을 확인한다. 이 조건이 성립하면 1을 반환하고, 그렇지 않으면 0을 반환한다.
정확성 (RSA) 🔗
이 오일러 정리에 의해 성립한다.
RSA 패딩: 확률론적 서명 표준 (RSA Padding: Probabilistic Signature Standard) 🔗
- 이전 공격을 방지하기 위해 특정 메시지 형식만 허용
- 확률론적 서명 표준(PSS)
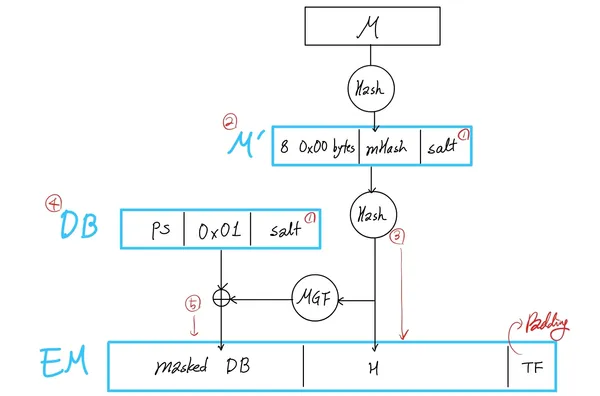
- 임의의 값 를 생성
- 고정 패딩 8개의 0x00 바이트, 해시 값 , 를 이어붙여 문자열 을 생성
- 를 계산
- 고정 패딩 , , 를 이어붙여 문자열 을 생성
- 고정 패딩 를 위해 인코딩된 메시지 을 생성
정리 (RSA PSS) 🔗
- RSA PSS는 확률론적 서명 표준으로, 이전 공격을 방지하기 위해 특정 메시지 형식만 허용한다.
- RSA PSS는 메시지 에 대해 를 이용하여 을 생성하고, 에 대한 해시값 를 계산한다.
- 를 이용하여 를 생성하고, 에 대한 마스킹된 값 를 계산한다.
- 를 이용하여 인코딩된 메시지 을 생성한다.
ElGamal 서명 (ElGamal Signature) 🔗
키 생성 (ElGamal) 🔗
- 큰 소수 와 의 큰 subgroup 생성자 를 선택
- 임의의 정수 를 선택
- 를 계산
- 공개 키 , 개인 키 를 반환
서명 (ElGamal Signature) 🔗
- 비밀 키 와 메시지 이 주어졌을 때
- 에서 임의의 원소 를 선택
- 와 을 계산
- 서명 를 반환
검증 (ElGamal Signature Verification) 🔗
- 공개 키 와 메시지 에 대한 서명 가 주어졌을 때
- 를 계산
- 를 확인한다. 이 조건이 성립하면 1을 반환하고, 그렇지 않으면 0을 반환한다.
정확성 (ElGamal Signature correctness) 🔗
보안성 (ElGamal Signature Security) 🔗
- 이산 로그 문제가 풀기 어려운 만큼 비밀 키 를 복구하기 어렵다.
- 존재적 위조 공격 (Existential Forgery Attack)
- 정수 를 선택하고 여기서 이어야 함
- 를 계산한다.
- 를 계산한다.
- 를 계산한다.
- 를 출력한다.
⇒ 그러면 이 성립하며 이므로
따라서 가 유효하다.
DSA 서명 (DSA Signature) 🔗
키 생성 (DSA) 🔗
- 순환 부분군 생성
- 소수 선택
- 는 소수 에 대한 유한체의 곱셈 군
- 의 순서란 이 군에 속하는 모든 원소의 개수:
- 는 의 소인수 중 하나인 소수
- 원소 개수가 인 부분군 를 생성
- 부분군 의 임의의 생성자 선택
- 에서 임의의 선택 후 계산
- 공개 키 , 개인 키 를 반환
서명 (DSA Signature) 🔗
비밀 키 와 메시지 이 주어졌을 때
- 에서 임의의 선택
- 계산
- 계산
- 서명 를 반환
검증 (DSA Signature Verification) 🔗
공개 키 와 메시지 에 대한 서명 가 주어졌을 때
- 를 확인
- 를 계산
- , 를 계산
- 를 계산
- 를 확인한다. 이 조건이 성립하면 1을 반환하고, 그렇지 않으면 0을 반환한다.