타원 곡선 암호화Elliptic Curve Cryptography
타원 곡선 암호화Elliptic Curve Cryptography
📅
곱셈 표기법 vs 덧셈 표기법 (Multiplication vs Additive) 🔗
| Multiplicative Notation | Operation | Additive Notation |
|---|---|---|
| Generator | ||
| Multiplication/Addition | ||
| Exponentiation/Scalar Multiplication |
곱셈 표기법은 주로 모듈러 연산과 같은 분야, 덧셈 표기법은 타원곡선 암호학과 같은 분야에서 사용된다.
예를 들어, 디피-헬만 키 교환에서는 곱셈 표기법을 사용하여 를 계산한다.
반면에 타원곡선 암호학에서는 덧셈 표기법을 사용하여 를 계산한다.
덧셈 표기법을 이용한 DSA (DSA with Additive Notation) 🔗
키 생성 (RSA Key Generation) 🔗
- 순서 를 가지는 (덧셈적) 순환 그룹 를 선택한다.
- 에서 생성자 를 선택한다.
- 에서 임의의 정수 를 선택한 후 를 계산한다.
- 공개 키 , 개인 키 를 반환한다.
서명 (DSA Signature) 🔗
개인 키 와 메시지 이 주어졌을 때
- 에서 임의의 를 선택한다.
- 와 를 계산한다.
- 서명 를 반환한다.
검증 (DSA Signature Verification) 🔗
공개 키 와 메시지 에 대한 서명 가 주어졌을 때
- 를 계산한다.
- 와 를 계산한다.
- 를 계산한다.
- 를 확인한다. 이 조건이 성립하면 1을 반환하고, 그렇지 않으면 0을 반환한다.
정확성 (DSA Signature correctness) 🔗
덧셈 표기법을 이용한 DSA에서 고려할 점 🔗
- (안전한)덧셈 그룹을 어떻게 생성할 것인가
- 모듈러 연산을 어떻게 처리할 것인가
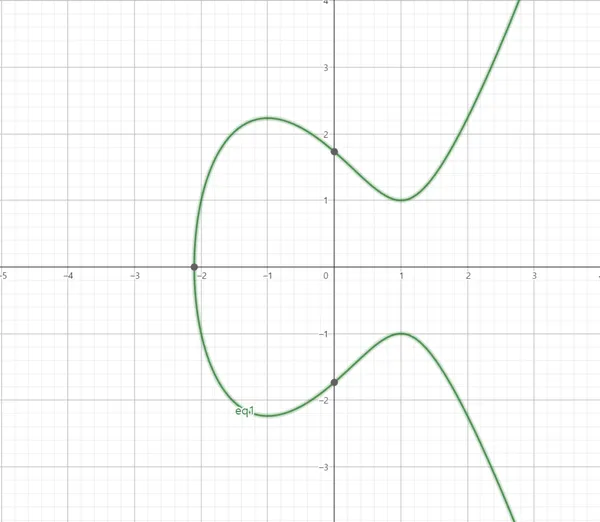
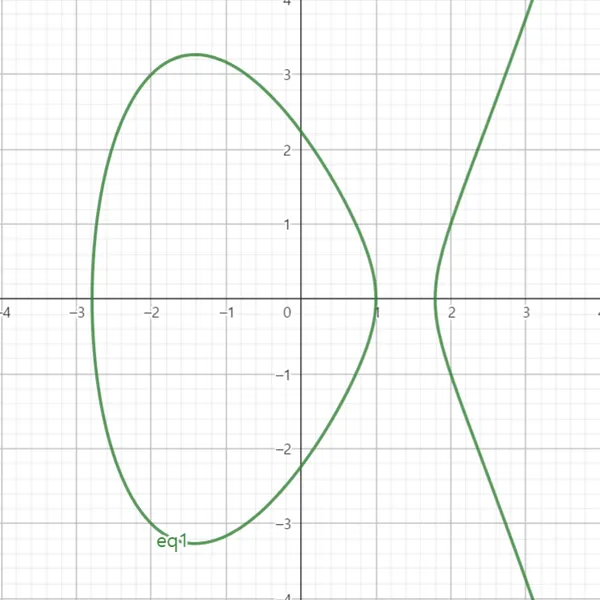
타원 곡선 (Elliptic Curve) 🔗
👨💻
Weierstrass 형태의 방정식 해 집합
여기서 상수 와 는 타원곡선의 계수로, 이어야 한다.
또한 타원곡선은 추가적인 점 을 가진다.
예시 (타원 곡선) 🔗
수학적 구조: 유한필드 (Mathematical Structure: Finite Field) 🔗
필드 는 덧셈, 곱셈 뺄셈, 그리고 0이 아닌 요소들에 대한 나눗셈이 가능한 수학적 구조이다. 또한 결합 법칙, 교환 법칙, 분배 법칙이 성립한다.
- 결합 법칙: ,
- 교환 법칙: ,
- 분배 법칙:
실수 집합, 복소수 집합은 필드이지만 정수 집합은 필드가 아니다.
는 가
소수
일 때 유한필드이다.
다항식 유한 필드 은 요소를 가지는 필드 (계수가 인 차수 의 다항식의 집합)이다.
(에서 는 차수 의 기약 다항식이다.)유한 필드 위의 타원곡선 (Elliptic Curve over Finite Field) 🔗
타원곡선은 유한필드 위에서 정의될 수 있다.
예시 (유한 필드 위의 타원곡선) 🔗
- 에 가 존재하지 않음
...
타원 곡선 위의 덧셈 정리 (Addition on Elliptic Curve Points) 🔗
타원곡선 위의 두 점 , 에 대해 를 계산하는 방법
👍
여기서 기울기 이다.
- 와 의 교점 찾기
- 세 근 의 합은 이다.
- 와 은 위에 있다.
예시 (타원곡선 위의 덧셈) 🔗
에서 두 점 과 가 주어졌을 때,
타원 곡선 덧셈은
ECC
(Elliptic Curve Cryptography)에서 사용되는 기본 연산이다.타원 곡선 위의 두 배 연산 (Doubling on Elliptic Curve Points) 🔗
타원곡선 위의 점 에 대해 를 계산하는 방법
👍
여기서 기울기 이다.
- 와 의 교점 찾기(덧셈 정리와 동일)
- 점 에서 접선의 기울기 계산하려면 의 도함수를 이용한다.
- 와 은 위에 있다.(덧셈 정리와 동일)
예시 (타원곡선 위의 두 배 연산) 🔗
에서 점 가 주어졌을 때,
타원 곡선 위의 스칼라 곱셈 (Scalar Multiplication on Elliptic Curve Points) 🔗
모듈러 거듭제곱을 위한 알고리즘을 고려해야 함
- 곱셈 덧셈 (ex: )
- 거듭제곱 두 배 연산 (ex: )
예시 (모듈러 거듭제곱을 위한 알고리즘) 🔗
Right to Left Algorithm
점 와 양의 정수 가 주어졌을 때,
R = O, T = P
for i from 0 to l-1 do
if x_i = 1 then
R = R + T
T = 2T
end for
return R타원 곡선의 장점 (Advantages of Elliptic Curve) 🔗
- 짧은 파라미터 크기
- 의 부분군 에서 정의된 DLP(이산 로그 문제) 해결
- 가 크지 않다면 가장 좋은 공격은 숫자 체 방법
- 가 크지 않다면 가장 좋은 공격은 Pollard Rho 방법
- 타원 곡선 위에서 정의된 DLP를 해결하기 위한 최선의 알고리즘은 Pollard Rho 방법
타원 곡선 DSA: ECDSA (Elliptic Curve Digital Signature Algorithm) 🔗
키 생성 (ECDSA Key Generation) 🔗
- 타원 곡선 를 사용하여 다음을 선택한다.
- 모듈러스
- 타원 곡선 계수 와
- 소수 차수 의 순환 그룹을 생성하는 점 (생성자)
- 에서 임의의 정수 를 선택한 후 를 계산한다.
- 공개 키 , 개인 키 를 반환한다.
서명 (ECDSA Signature) 🔗
개인 키 와 메시지 이 주어졌을 때
- 에서 임의의 를 선택한다.
- 를 계산한 후 (점 의 좌표)를 둔다.
- 를 계산한다.
- 서명 를 반환한다.
검증 (ECDSA Signature Verification) 🔗
공개 키 와 메시지 에 대한 서명 가 주어졌을 때
- 를 계산한다.
- 와 를 계산한다.
- 를 계산한다.
- 를 확인한다. 이 조건이 성립하면 1을 반환하고, 그렇지 않으면 0을 반환한다.
정확성 (ECDSA Signature correctness) 🔗
의 좌표 = 의 좌표
추가> 타원 곡선 ElGamal (Elliptic Curve ElGamal) 🔗
키 생성 (EC ElGamal Key Generation) 🔗
- 타원 곡선 를 사용하여 다음을 선택한다.
- 모듈러스
- 타원 곡선 계수 와
- 소수 차수 의 순환 그룹을 생성하는 점 (생성자)
- 에서 임의의 정수 를 선택한 후 를 계산한다.
- 공개 키 , 개인 키 를 반환한다.
암호화 (EC ElGamal Encryption) 🔗
공개 키 와 평문 이 주어졌을 때
- 에서 임의의 원소 를 선택한다.
- , 를 계산한다.
- 암호문 를 반환한다.
복호화 (EC ElGamal Decryption) 🔗
개인 키 와 암호문 가 주어졌을 때
- 를 계산한다.()
- 평문 을 반환한다.