 해시 함수Hash Function
해시 함수Hash Function
📅
해시 함수란 (What is a Hash Function) 🔗
임의의 크기의 데이터를 입력받아 고정된 크기의 출력을 반환하는 함수
-
예시: 비트별 XOR
Bit 1 Bit 2 ... Bit n Block 1 ... Block 2 ... ... ... ... ... ... Block m ... Hash Output ... ex. 두 개의 블록 / 을 XOR하여 을 반환
암호학적 해시 함수 (Cryptographic Hash Function) 🔗
임의 길이의 메시지를 입력받아고정된 길이의 메시지 다이제스트를 출력하는 함수
암호학적 해시 함수는 다음 조건을 만족해야 함
- 효율적 계산(Computational Efficiency)
- 입력 이 주어지면 을 효율적으로 계산할 수 있어야 함
- 단방향성or원본 숨김 저항성(One-way or Pre-image Resistance)
- 가 주어졌을 때 를 만족하는 을 찾는 것이 계산적으로 불가능해야 함
- 제2 원본 숨김 저항성or약한 충돌 저항성(Second Pre-image Resistance or Weak Collision Resistance)
- 이 주어졌을 때 을 만족하는 을 찾는 것이 계산적으로 불가능해야 함
- 충돌 저항성(Collision Resistance)
- 이 주어졌을 때 을 만족하는 을 찾는 것이 계산적으로 불가능해야 함
예시: MD5, HAVAL-128, SHA-1,
SHA-2
, SHA-3SHA-1 및 SHA-2의 설계 논리 (Design Rationale of SHA-1 and SHA-2) 🔗
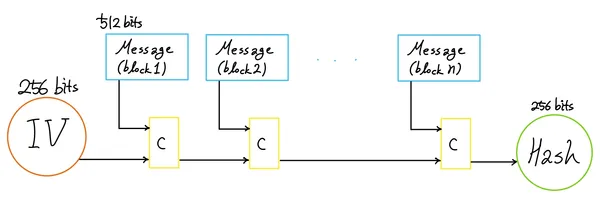
- 초기화 벡터 (IV: Initialization Vector)
- 메시지 블록 (Message Block)
- 압축 함수:c (Compression Function)
- 해시 출력 (Hash Output)
SHA-1과 SHA-2의 라운드 함수 (Round Function of SHA-1 and SHA-2) 🔗
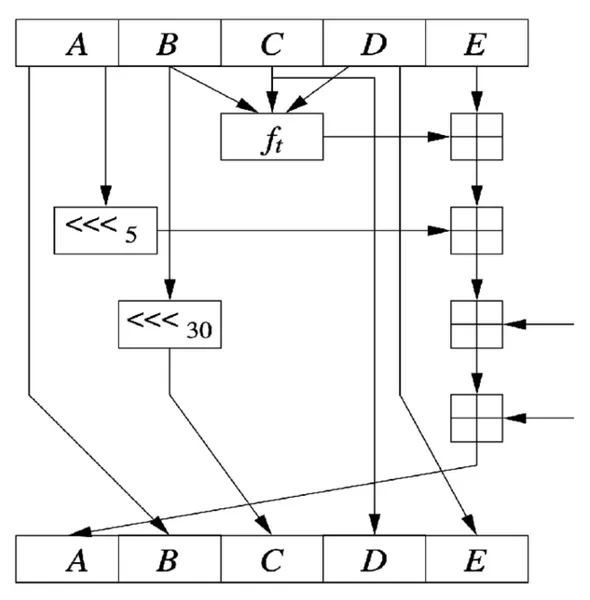
- 초기값
- 라운드 함수
- - 라운드 번호 에 따라 다른 논리 연산 수행
- 비트 순환 이동
- 와 비트는 각각 5 비트와 30비트 순환 이동
- 순환 이동은 비트를 왼쪽으로 회전시키며, 가장 왼쪽 비트는 가장 오른쪽 비트로 이동
- 연산 및 업데이트
- 각 라운드에서 는 각각 와 다른 연산을 통해 갱신됨
- 와 같은 식으로 갱신
예: 첫 라운드에서 다음과 같은 연산 수행
- (기존 값을 에 저장)
SHA-3의 설계 논리 (Design Rationale of SHA-3) 🔗
스펀지 구조 기반: 데이터가 흡수된 후 결과 압축
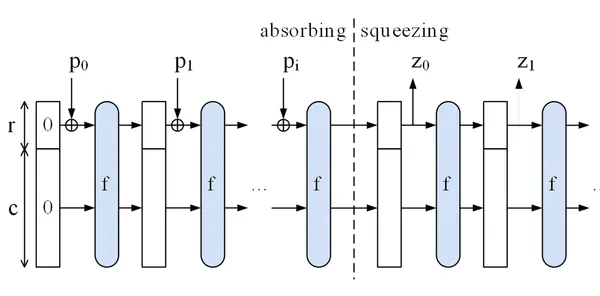
- 는 블록 순열을 위한 함수로, XOR, AND, NOT 연산으로 구성됨