 소스 코딩Source Coding
소스 코딩Source Coding
📅
개요 (Introduction) 🔗
- 소스 심볼은 이진수로 인코딩 되어야 한다.
- 평균 코드 길이는 최소화되어야 한다.
- 중복 제거 비트율 감소
- 알파벳에 기반한 이산 무기억 소스 고려 :
- 의 확률:
- 의 코드 길이:
- 평균 코드 길이(심볼 당 평균 비트 수):
- 의 최소한 가능한 값:
- 소스의 코딩 효율성:
- 데이터 압축
- 전송 전에 중복 정보 제거
- 손실 없는 데이터 압축
- 이산 무기억 소스(discrete memoryless source)의 출력을 나타내는 소스코드는 유일하게 복호화 가능
데이터 압축을 위한 소스 코딩 체계(Source Coding Schemes for Data Compression) 🔗
접두사 코딩(Prefix Coding) 🔗
다른 코드의 접두어가 아닌가변 길이 소스 코드
- 접두사 코드의 특성
- 접두사 코드는 유일하게 복호화 가능
- 접두사 코드의 역은 항상 참이 아님 → 모든 유일하게 복호화할 수 있는 코드가 접두사 코드인 것은 아님
예시 (접두사 코드) 🔗
| 심볼 | 발생 확률 | 코드 I | 코드 II | 코드 III |
|---|---|---|---|---|
| s0 | 0.5 | 0 | 0 | 0 |
| s1 | 0.25 | 1 | 10 | 01 |
| s2 | 0.125 | 00 | 110 | 011 |
| s3 | 0.125 | 11 | 111 | 0111 |
Code1: 접두사 코드 X
Code2: 접두사 코드 O
Code3: 유일하게 복호화 가능 but 접두사 코드 X - 다음 코드의 시작을 구분하기 힘들다
ex) Code2
0101110111 -> 0/10/111/0/111 -> unically decodable(유일하게 복호화 가능)
결정 트리
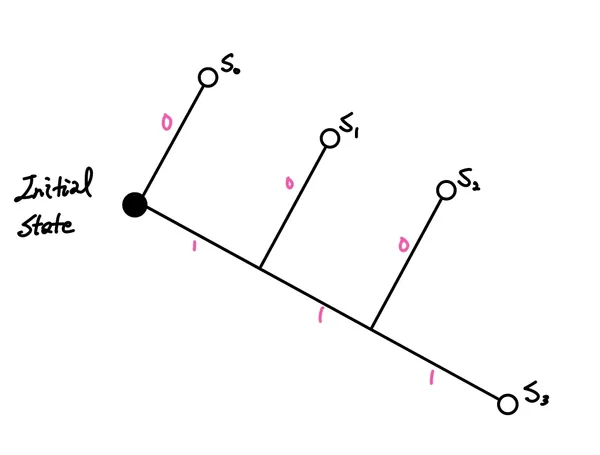
임의의 심볼 는 확률 로 발생
- 확률들의 총합:
- 평균 코드 길이:
* 허프먼 코딩 (Huffman Coding) 🔗
⭐
중요
⭐허프먼 코딩 알고리즘 🔗
데이터 압축에 자주 사용되는 방법으로, 자주 등장하는 기호에는 짧은 부호를 할당하고 드물게 등장하는 기호에는 긴 부호를 할당하여
데이터를 압축
한다.- 기호 확률을 감소하는 순서로 배열 후 트리의 리프 노드로 간주
- 노드가 하나 이상 남을 때 까지 다음을 반복
- 가장 낮은 확률을 가진 두 노드를 선택 후 가장 낮은 노드에는 0, 높은 노드에는 1을 할당(반대도 가능, but 일관적이어야 함)
- 두 노드를 병합하여 하나의 노드 생성, 그 확률은 두 노드의 확률의 합이 됨
- 1단계로 돌아가기
- 각 기호에 대해, 리프 노드에서 트리의 루트까지의 경로를 따라 이진 코드 생성
- 리프 노드의 비트는 부호어(codeword)의 마지막 비트가 된다.
허프먼 코드의 특징 🔗
접두사 코드
각 기호의 부호어 길이는 전달하는 정보의 양과 대략 같다
확률 분포가 알려지고 정확할 경우, 허프먼 코드는 매우 효과적임
- 분산은 부호어 길이의 변동성을 측정하는 것
- 오류를 피하고자 분산이 큰허프먼 트리를 선택 → 분산이 높은 트리는 부호의 길이가 더 다양하므로 오류를 더 잘 처리할 수 있다.
허프먼 트리 구성 예시 (Example of Huffman Tree Construction) 🔗
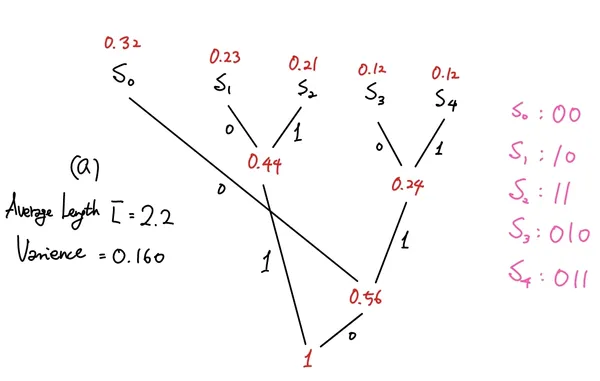
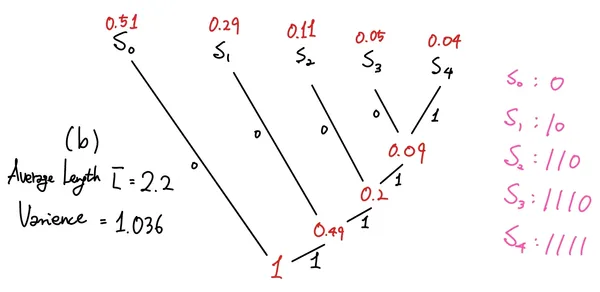
두 트리 모두 같은 평균 길이를 가지지만
분산
은 다르다.- 분산이 높은 트리는 오류를 더 잘 처리할 수 있다.