채널 코딩 | PromleeBlog

🚀

디지털 통신 시스템에서의 채널 코딩 (Channel Coding in Digital Communication Systems) 🔗

전송할 정보

\rightarrow

소스 코딩

\rightarrow

채널 코딩

\rightarrow

변조

\rightarrow

송신기

\rightarrow

채널

\rightarrow

수신기

\rightarrow

복조(Demodulation)

\rightarrow

채널 디코딩

\rightarrow

소스 디코딩

\rightarrow

수신된 정보

🚀

전방 오류 정정: FEC (Forward Error Correction) 🔗

수신기가 스스로 오류를 복구할 수 있도록 충분한
중복 데이터
를 전송하는 것, 송신자의 재전송이 필요하지 않다.

ARQ

(Automatic Repeat reQuest): 수신기가 오류를 감지하면 송신기에 재전송을 요청하는 방법

FEC의 주요 범주:

블록 코드

, 합동 코드, 선형 블록 코드, 사이클릭 코드, 컨볼루션 코드, 터보 코드, LDPC(Low-Density Parity-Check) 코드

🚀

* 블록 코드 (Block Codes) 🔗

중요!

정보를 길이 $k$ 비트의 블록 단위로 처리하는 코드

r

패리티 비트 또는 검사 비트가 각 블록에 추가됨. 총 길이는

n = k + r

코드율

(Code rate)

R = \frac{k}{n}

채널이 좋을 때는 코드율을

낮추고

, 채널이 나쁠 때는 코드율을

높이는

것이 좋다.

디코더는

n

비트의 수신 신호를 받아

k

비트의 정보를 복구

효율성, 신뢰성, 인코딩/디코딩 복잡성 간에 트레이드오프 존재

✅

선형 블록 코드 (Linear Block Codes) 🔗

블록 코드의 부분 집합이
벡터 공간
을 형성하는 코드

선형 블록 코드의

C=mG

G: 생성 행렬, m: 정보 단어, C: 부호어
- C
  : $C = (c_1, c_2, ..., c_k, c_{k+1}, ..., c_n) , C = (m | c_p), c_p = mP$
- m
  : 인코딩되지 않은 메시지 벡터 $m = [m_1, m_2, \ldots, m_k]$
- G
  : $[I | P]$ , $P = \begin{bmatrix}p_{11} & p_{12} & ... & p_{1(n-k)} \\p_{21} & p_{22} & ... & p_{2(n-k)} \\... & ... & ... & ... \\p_{k1} & p_{k2} & ... & p_{k(n-k)}\end{bmatrix}= \begin{bmatrix}p_1 \\p_2 \\... \\p_k\end{bmatrix}$

여기서

p_i = \text{Remainder of}\; [x^{n-k+i-1} / g(x)]\; for \; i = 1, 2, ..., k

, 그리고

I

는 단위 행렬이다.

g(x)

생성 다항식

패리티 검사 행렬

H = [P^T | I]

메시지 벡터(m) $\rightarrow$ 생성 행렬(G) $\rightarrow$ 부호어(C)
부호어(C) $\rightarrow$ 패리티 검사 행렬( $H^T$ ) $\rightarrow$ null 벡터(0)

➡️

생성 행렬
과
패리티 검사 행렬
연산 🔗

패리티 검사 행렬

H

는 수신된 부호에서 오류를 감지하기 위해

c \ast H^T = 0

(영벡터)이라는 사실을 사용한다.

$C \cdot H^T = (m \cdot G) \cdot H^T = m \cdot (G \cdot H^T)$
$= m [I|P] \cdot \begin{bmatrix} P \\I \end{bmatrix} = m \cdot [I\cdot P + P\cdot I] = m \cdot [P \oplus P] = m \cdot 0 = 0$

x = c \oplus e

가 수신된 메시지일 때, 여기서

c

는 올바른 부호이고

e

는 오류이다.

신드롬

S = x \ast H^T = (c \oplus e) \ast H^T = c \ast H^T \cdot e \ast H^T = e \ast H^T

를 계산하여 구한다.

만약 $S$ 가 0이면 메시지는 정확하고, 그렇지 않으면 오류가 포함되어 있으며, 일반적으로 알려진 오류 패턴을 통해 올바른 메시지를 디코딩할 수 있다.

➡️

예제 (선형 블록 코드) 🔗

선형 블록 코드 인코더 G를 찾기.

코드 생성 다항식:

g(x) = x^3 + x + 1

코드 길이:

n = 7

, 정보 비트:

k = 4

해결

생성 행렬

G = [I|P] = \begin{bmatrix} 1 & 0 & 0 & 0 & p_1 \\ 0 & 1 & 0 & 0 & p_2 \\ 0 & 0 & 1 & 0 & p_3 \\ 0 & 0 & 0 & 1 & p_4 \end{bmatrix}

여기서

p_i = \text{Remainder of}\; [x^{n-k+i-1} / g(x)]\; for \; i = 1, 2, ..., k

에 대해, 그리고

I

는 단위 행렬이다.

p_1 = \text{나머지} \left[ \frac{x^3}{1+x+x^3} \right] = 1+x \rightarrow [110] \\ p_2 = \text{나머지} \left[ \frac{x^4}{1+x+x^3} \right] = x+x^2 \rightarrow [011] \\ p_3 = \text{나머지} \left[ \frac{x^5}{1+x+x^3} \right] = 1+x+x^2 \rightarrow [111] \\ p_4 = \text{나머지} \left[ \frac{x^6}{1+x+x^3} \right] = 1+x^2 \rightarrow [101] \\ \\ G = \left[ \begin{array}{cccc|ccc} 1 & 0 & 0 & 0 & 1 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 & 1 & 0 & 1 \end{array} \right]

패리티 체크 행렬

H = [P^T | I] = \left[ \begin{array}{cccc|ccc} 1 & 0 & 1 & 1 & 1 & 0 & 0 \\ 1 & 1 & 1 & 0 & 0 & 1 & 0 \\ 0 & 1 & 1 & 1 & 0 & 0 & 1 \end{array} \right]

메시지 벡터

m = [1, 0, 1, 1]

에 대하여,

부호어

C = m \cdot G = [1, 0, 1, 1] \cdot \left[ \begin{array}{cccc|ccc} 1 & 0 & 0 & 0 & 1 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 & 1 & 1 \\ 0 & 0 & 1 & 0 & 1 & 1 & 1 \\ 0 & 0 & 0 & 1 & 1 & 0 & 1 \end{array} \right] = [1, 0, 1, 1, 1, 0, 0]

패리티 검사

C \cdot H^T = [1, 0, 1, 1, 1, 0, 0] \cdot \left[ \begin{array}{} 1 & 1 & 0 \\ 0 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array} \right] = [0, 0, 0]

🚀

컨볼루션 코드 (Convolutional Codes) 🔗

블록 코드와 달리,
시간적인 정보
를 이용하여
연속적인
정보를 처리하는 코드

정보 블록이 아닌 정보 스트림을 인코딩함

특정 정보 symbol의 값이 다음

M

개의 symbol의 값에 영향을 줌 - 메모리 길이

M

시프트 레지스터를 사용한 쉬운 구현

k

개의 입력과

n

개의 출력을 가정

디코딩은 대부분

Viterbi 알고리즘

을 사용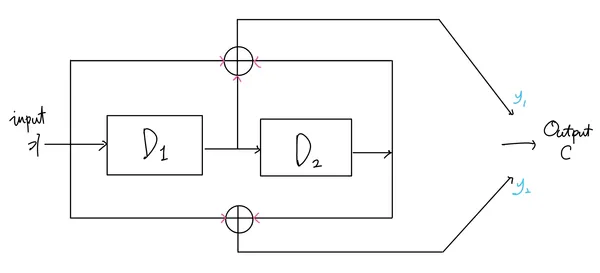

n

= 2,

k

= 1,

M

= 2인 컨볼루션 코드의 예시

입력

x

는 D1, D2 레지스터를 거쳐 두 개의 출력

y_1

과

y_2

를 생성

D1, D2의 초기값은 0이다.

y_1 = x \oplus D1 \oplus D2

y_2 = x \oplus D2

D1의 다음 상태는

x

이고,

D2

의 다음 상태는

D1

이다.

예시 입력이 (1, 1, 1, 0, 0, 0)일 때,

$x$	$D1$	$D2$	$y_1$	$y_2$
1	0	0	1	1
1	1	0	0	1
1	1	1	1	0
0	1	1	0	1
0	0	1	1	1
0	0	0	0	0

예시 입력이 (1, 0, 1, 0, 0, 0)일 때,

$x$	$D1$	$D2$	$y_1$	$y_2$
1	0	0	1	1
0	1	0	1	0
1	1	1	0	0
0	1	1	1	1
0	0	1	1	1
0	0	0	0	0

🚀

인터리빙 (Interleaving) 🔗

오류의 영향을 분산시키기 위해 사용되는 기술

입력 데이터

a_1, a_2, ..., a_n

인터리빙 과정

에서의 재배치

\left[ \begin{array} {} a_1 & a_2 & a_3 & a_4 \\ a_5 & a_6 & a_7 & a_8 \\ ... & ... & ... & ... \\ a_{n-3} & a_{n-2} & a_{n-1} & a_n \end{array} \right]

→ 가로방향: 쓰기, 세로 방향: 읽기

전송 데이터

a_1, a_5, ..., a_2, a_6, ..., a_3, a_7, ..., a_4, a_8, ...

디 인터리빙

과정에서의 재배치

\left[ \begin{array} {} a_1 & a_2 & a_3 & a_4 \\ a_5 & a_6 & a_7 & a_8 \\ ... & ... & ... & ... \\ a_{n-3} & a_{n-2} & a_{n-1} & a_n \end{array} \right]

→ 가로방향: 읽기, 세로 방향: 쓰기

출력 데이터

a_1, a_2, ..., a_n

✅

예시 (인터리빙) 🔗

전송 데이터: 0, 0, 0,

, 0, 0, 0, ...

디 인터리빙 데이터:

\left[ \begin{array} {} 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 1&0&0&0 \end{array} \right]

출력 데이터: 0,

, 0, 0, 0,

, 0, 0,

, ...

밑줄쳐진 오류 코드가 인터리빙을 통해 분산되어 전송됨 → 각 오류는 서로 다른 위치에 전송되어 오류를 복구할 수 있음

🚀

정보 용량 이론: 샤논 한계 (Information Capacity Theory: Shannon Limit) 🔗

대역폭

B

Hz를 갖는 연속 채널의 정보 용량

C

는 전력 스펙트럼 밀도가

N_0/2

인 가산성 백색 잡음으로 방해받을 수 있다.

대역폭

B

가 아래 조건을 만족할 때,

C = B \log_2(1 + \frac{P}{N_0} )

bits/sec

P

는 평균 전송 전력이고,

E_b

는 비트 당 전송 에너지,

R_b

는 전송 속도

P = E_b \cdot R_b

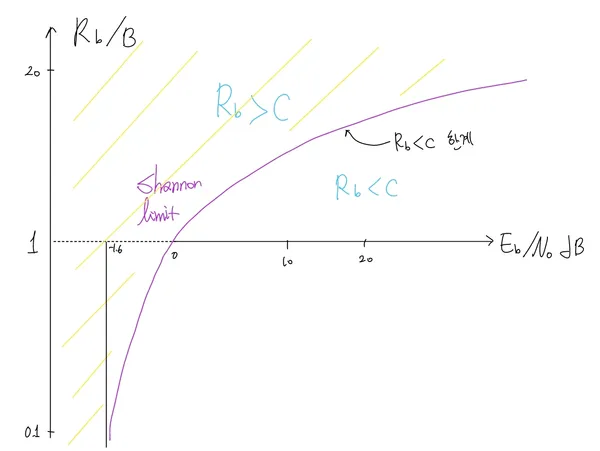
수평축:

E_b/N_0

비트당 에너지 대 잡음 전력 밀도
이 수치가 클수록 채널을 통해 더 높은 비트율로 데이터 전송이 가능하다.

수직축:

R_b/B

비트율 대 대역폭
이 수치는 채널을 통해 단위 대역폭 당 전송할 수 있는 정보의 양을 나타낸다.

추천 포스트

채널 코딩Channel Coding