 결정 트리Decision Tree
결정 트리Decision Tree
📅
지도 기계 학습 (Supervised Machine Learning) 🔗
Setting
- : data(observation)
- : label(class)
Goal
가 주어졌을 때, 를 예측하는 함수 를 찾는 것
: 의 근사함수 error
: loss function
ex)
이 되도록 찾아야 함training data
: loss of training data
: porbability function Naive Bayes
: tree-like function Decision Tree
: neuron-like function CNNDecision Tree 🔗
Root node: 전체 데이터 집합
Internal node: 데이터 집합을 분할하는 데 사용되는
특징
Leaf node: 분할된 데이터 집합에 대한 라벨(클래스)
결정 트리
는 특성 공간을 축에 평행한 사각형
으로 나눈다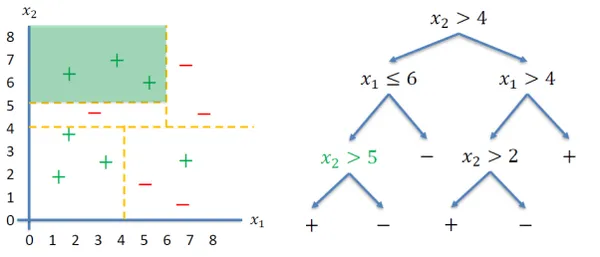
결정 트리 학습 (Decision Tree Learning) 🔗
결정 트리 학습 알고리즘
(Decision Tree Learning Algorithm)- 데이터 집합을 가장 잘 나눌 수 있는 특징을 선택 좋은 특징을 고르는 방법? - 데이터가 나눠진 후 불순도가 가장 낮은 특징을 선택(같은 클래스로 이루어진 데이터가 많이 모이는 특징)
- 선택된 특징의 값을 기준으로 데이터 집합을 나눈다 좋은 값을 판단하는 방법?
불확실성 측정 (Measure of Uncertainty) 🔗
결정론적 분포가 좋음(Deterministic Good)
, , ,
균등 분포가 나쁨(Uniform Distribution Bad)
, , ,
그 사이의 분포는?
, , ,
엔트로피 (Entropy) 🔗
확률 변수의 불확실성을 측정하는 방법
확률 변수 의 엔트로피
불확실성이 높을수록 엔트로피가 높다
성질:
- 최대값: 가 균등 분포일 때 (완전 불확실) ex. ,
- 최소값: 0 (완전 확실) ex. ,
높은 엔트로피, 낮은 엔트로피 (High Entropy, Low Entropy) 🔗
높은 엔트로피 (High Entropy)
- 가 균등한 분포에서 나온 경우
- 히스토그램이 평평함
- 이로부터 샘플링된 값들은 예측하기 어려움
낮은 엔트로피 (Low Entropy)
- 가 다양한 분포 (피크와 계곡이 있는 분포)에서 나온 경우
- 히스토그램에 많은 낮음과 높음이 있음
- 이로부터 샘플링된 값들은 예측하기 쉬움
목표
- 엔트로피를 줄이는 특징을 선택하여 데이터를 분할
엔트로피 예제 (Entropy Example) 🔗
| T | T | T |
|---|---|---|
| T | F | T |
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
조건부 엔트로피 (Conditional Entropy) 🔗
👨💻
조건부 엔트로피 : 확률 변수 가 확률 변수 에 조건부일 때의 엔트로피
예제 (조건부 엔트로피) 🔗
| T | T | T |
|---|---|---|
| T | F | T |
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
,
- 이 T일 때, ,
- ,
- 이 F일 때, ,
- ,
Entropy of after split using (0.19 0.1)
,
- 이 T일 때, ,
- ,
- 이 F일 때, ,
- ,
Entropy of after split using (0.19 0.03)
를 사용하여 데이터를 나누는 것이 더 좋은 결과를 가져옴(엔트로피를 줄임)
정보 이득 (Information Gain) 🔗
분할 후 엔트로피(불확실성)의 감소
위의 예제에서,
- 은 분할에 유용한특징
- 는 분할에 더 유용한특징
결정 트리 학습 알고리즘 (Decision Tree Learning Algorithm) 🔗
- 빈 결정 트리에서 시작
- 노드를 만들고 정보 이득(IG)에 기반하여 좋은 특징을 선택
- 선택된 특징을 사용하여 데이터 집합을 분할
- 분할된 데이터 집합에 대해 재귀적으로 반복
- 모든 데이터가 같은 클래스에 속하거나 더 이상 특징이 없을 때까지 반복
- only a single label
무작위 포레스트 (Random Forest) 🔗
부트스트랩 집계(Bootstrap Aggregating)를 사용하여 많은 결정 트리를 학습시킴
무작위로 n개의 예제 부분 샘플링
부분 샘플링한 데이터 집합을 사용하여 결정 트리를 학습
학습된 트리들 간의 평균 또는 다수결 투표를 사용하여 예측
랜덤 포레스트
예측 결합
: 예측 변수
: 결정 트리의 예측 변수
랜덤 포레스트
예측 변수의 분산
: 라벨의 불확실성
랜덤 포레스트의 예측 변수가 더 안정적