 신호 공간Signal Space
신호 공간Signal Space
📅
신호 공간이란? (What is Signal Space?) 🔗
신호 공간이란?
- 신호 공간: 신호를 N차원 벡터로 표현하는 공간
- Constallation(별자리)이라고도 함
신호 공간이 필요한 이유
- 신호를 벡터로 변환하고 그 반대의 과정을 가능하게 함
- 신호 간 에너지와유클리드 거리를 구할 수 있다.
왜 신호 간 유클리드 거리에 관심을 가지는가
- 감지 목적: 수신된 신호를 벡터로 변환
- 수신된 신호와 최소 거리에 있는 신호를 전송된 신호로 추정함
신호 공간 개념도 (Schematic example of Signal Space) 🔗
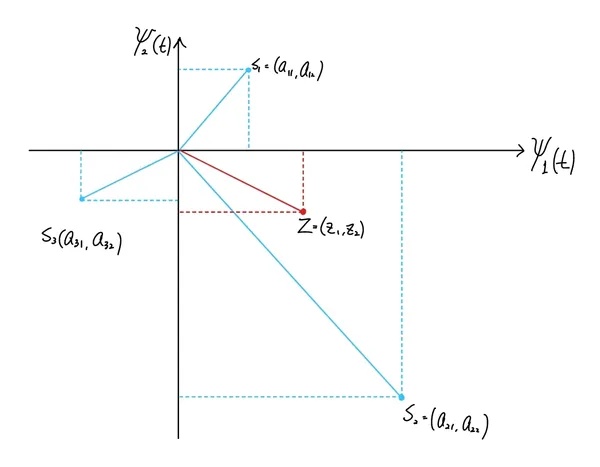
전송된 신호의 대안들
일치 필터 출력에서 수신된 신호
- 벡터와 각 벡터 사이의 거리를 계산하여, 수신된 신호가 전송된 신호와 얼마나 가까운지 판단
- 거리가 가장 작은 를 전송된 신호로 추정
신호 공간 형성 (Signal Space Formation) 🔗
신호 공간을 형성하기 위해선 두 신호 간의 내적을 알아야 함
-
내적(스칼라 곱): 는 와 간의 교차 상관 관계를 나타낸다.
- 는 의 켤레 복소수
내적의 성질:
신호 공간에서 거리는 norm을 계산하므로써 측정됨
- 신호의 norm: 의길이
- 두 신호 간의 norm: 두 신호 사이의 거리를유클리드 거리라고 한다.
예시 (신호 공간에서의 거리 계산) 🔗
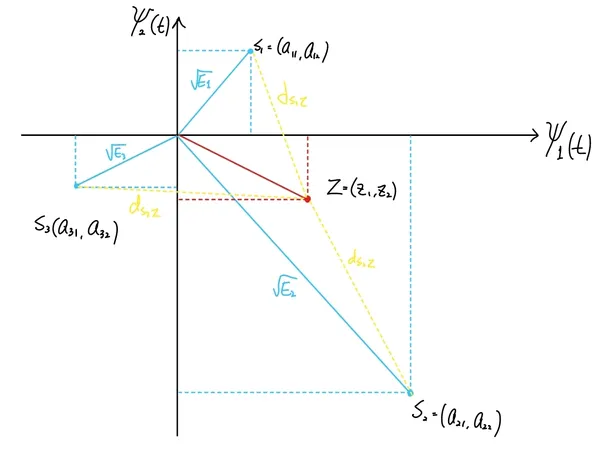
신호 와 사이의 유클리드 거리:
정규 직교 신호 공간 (Orthogonal Signal Space) 🔗
N차원 직교 신호 공간은 N개의 선형 독립적인 기저 함수 에 의해 정의된다.
이 기저 함수들은 직교성 조건을 만족해야 한다.
여기서
- 모든 이면, 신호 공간은 정규 직교(orthonormal)이다.
- 비정규 직교 세트로부터 정규 직교 기저를 구성하는 방법:
- 그램-슈미트 방법론 사용
예시 (정규 직교 신호 공간) 🔗
2차원
정규 직교 신호 공간
- 반각공식 사용
1차원
정규 직교 신호 공간- (0부터 T까지 일정한 값)
- (정규화)
예제: BPSK (Binary Phase Shift Keying) 🔗
Q. 이진 위상 변조 키잉(BPSK) 변조는 신호 , 로 1 비트를 전송하고, , 로 0 비트를 전송한다. 이 변조에 대한 정규 직교 기저 함수와 계수 를 찾아라.
A. 이 변조에는 단 하나의 기저 함수 가 있으며, 정규화를 위해 가 필요하다. 계수는 와 로 주어진다.
BPSK에는
두 개의 신호
, 하나의 차원
이 있다. 따라서, 이 신호 공간은 1차원이다.신호 집합을 직교 벡터로 표현 (Representation of Signal Set as Orthogonal Vectors) 🔗
임의의 유한한 파형 집합 은 각 요소가 시간 T 동안 지속되며, N개의 직교 파형 의 선형 조합으로 표현될 수 있다. (여기서 )
여기서
-
- 는 파형의 벡터 표현이다.
- 파형 에너지
직교 진폭 변조 (Quadrature Amplitude Modulation, QAM) 🔗
QAM은 진폭 변조와 위상 변조를 결합한 변조 방식으로, 복소수 신호 공간을 사용하여 다수의 비트를 동시에 전송할 수 있다.
90도 위상차를 가지는 두 개의 신호를 사용하여, 2차원 신호 공간을 형성한다.
예를 들어, 16-QAM의 성좌도는 다음과 같다.
각 점은 4개의 비트 정보를 나타내며, 각각 다른 진폭 조합을 나타낸다.